Question

Three distinct points A, B and C are given in the 2-dimensional plane such that the ratio of the distance of any of them from the point $(1,0)$ to the distance from the point $(-1,0)$ is equal to $\dfrac{1}{3}$. Then the circumcentre of triangle ABC is at the point
A) $(0,0)$
B) $\left( \dfrac{5}{4},0 \right)$
C) $\left( \dfrac{5}{2},0 \right)$
D) $\left( \dfrac{5}{3},0 \right)$

Answer 1

Hint: A circle on which the three vertices of a triangle lie is called the circumcircle of the triangle and the centre of this circle is called the circumcentre.

The given triangle is $\Delta ABC$.
We will consider $\left( h,k \right)$ to be coordinates of one of the vertices .
First , we need to find the distance of $\left( h,k \right)$ from $(1,0)$and $(-1,0)$.
We know that the distance between the two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ given as $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$

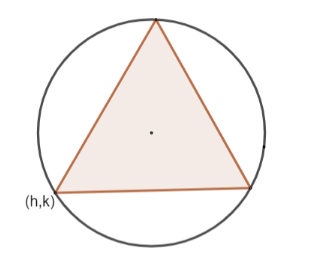
So , to find the distance of $\left( h,k \right)$ from $(1,0)$, we will substitute $\left( h,k \right)$ in place of $\left( {{x}_{2}},{{y}_{2}} \right)$and $(1,0)$ in place of $\left( {{x}_{1}},{{y}_{1}} \right)$ in the distance formula .
So, the distance of $\left( h,k \right)$ from $(1,0)$ is given as
${{d}_{1}}=\sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-0 \right)}^{2}}}$
$\Rightarrow {{d}_{1}}=\sqrt{{{\left( h-1 \right)}^{2}}+{{k}^{2}}}.......(i)$
Also , to find the distance of $\left( h,k \right)$from $(-1,0)$, we will substitute $\left( h,k \right)$ in place of $\left( {{x}_{2}},{{y}_{2}} \right)$ and $(-1,0)$ in place of $\left( {{x}_{1}},{{y}_{1}} \right)$ in the distance formula .
So, the distance of $\left( h,k \right)$ from $(-1,0)$is given as
${{d}_{2}}=\sqrt{{{\left( h+1 \right)}^{2}}+{{\left( k-0 \right)}^{2}}}$
$\Rightarrow {{d}_{2}}=\sqrt{{{\left( h+1 \right)}^{2}}+{{k}^{2}}}........(ii)$
Now, in the question it is given that the ratio of distance of vertex from $(1,0)$ to the distance of vertex from $(-1,0)$ is equal to $\dfrac{1}{3}$.
So , $\dfrac{{{d}_{1}}}{{{d}_{2}}}=\dfrac{1}{3}$
$\Rightarrow \dfrac{\sqrt{{{\left( h-1 \right)}^{2}}+{{k}^{2}}}}{\sqrt{{{\left( h+1 \right)}^{2}}+{{k}^{2}}}}=\dfrac{1}{3}$
Now , we will square both sides to remove the square root sign .
On squaring both sides , we get

& \dfrac{{{\left( h-1 \right)}^{2}}+{{k}^{2}}}{{{\left( h+1 \right)}^{2}}+{{k}^{2}}}=\dfrac{1}{9} \\\ & \Rightarrow 9{{\left( h-1 \right)}^{2}}+9{{k}^{2}}={{\left( h+1 \right)}^{2}}+{{k}^{2}} \\\ & \Rightarrow 9\left( {{h}^{2}}+1-2h+{{k}^{2}} \right)={{h}^{2}}+1+2h+{{k}^{2}} \\\ & \Rightarrow 9{{h}^{2}}+9-18h+9{{k}^{2}}={{h}^{2}}+2h+1+{{k}^{2}} \\\ & \Rightarrow 8{{h}^{2}}+8{{k}^{2}}-20h+8=0 \\\ \end{aligned}$$ Taking $$8$$ common from the LHS , we get $$8\left[ {{h}^{2}}+{{k}^{2}}-\dfrac{5}{2}h+1 \right]=0$$ $$\Rightarrow {{h}^{2}}+{{k}^{2}}-\dfrac{5}{2}h+1=0$$ Now , we can write $1$ as $\dfrac{16}{16}$ , which can further be written as $\dfrac{25}{16}-\dfrac{9}{16}$. So, $${{h}^{2}}+{{k}^{2}}-\dfrac{5}{2}h+1=0$$ can be written as $${{h}^{2}}-\left( 2\times \dfrac{5}{4}\times h \right)+{{\left( \dfrac{5}{4} \right)}^{2}}-\dfrac{9}{16}+{{k}^{2}}=0$$ $$\begin{aligned} & \Rightarrow {{\left( h-\dfrac{5}{4} \right)}^{2}}+{{k}^{2}}-\dfrac{9}{16}=0 \\\ & \Rightarrow {{\left( h-\dfrac{5}{4} \right)}^{2}}+{{k}^{2}}=\dfrac{9}{16} \\\ \end{aligned}$$ Now, the locus of $$(h,k)$$ is given by replacing $$(h,k)$$by $$(x,y)$$. So, the locus of the vertex of the triangle $$\Delta ABC$$ is given as, $${{\left( x-\dfrac{5}{4} \right)}^{2}}+{{y}^{2}}={{\left( \dfrac{3}{4} \right)}^{2}}.....(iii)$$ Now, we know the equation of the circle with centre at $$(a,b)$$ and radius $$r$$ is given as $${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}......(iv)$$ Comparing equation $$(iii)$$and$$(iv)$$, we can conclude that the locus of vertex of the triangle $$\Delta ABC$$ is a circle with centre at $$\left( \dfrac{5}{4},0 \right)$$ and radius $$\dfrac{3}{4}$$units. Now , we know , the circle on which all the three vertices of a triangle lie is known as the circumcircle and its centre is known as the circumcentre . So , circumcentre of $$\Delta ABC$$ is $$\left( \dfrac{5}{4},0 \right)$$ Option (b) $$\left( \dfrac{5}{4},0 \right)$$ is correct. Note: The distance between two points $$({{x}_{1}},{{y}_{1}})$$ and $$({{x}_{2}},{{y}_{2}})$$ is given as $$d=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}$$ and not $$d=\sqrt{{{({{x}_{1}}+{{x}_{2}})}^{2}}+{{({{y}_{1}}+{{y}_{2}})}^{2}}}$$. It is a very common mistake made by students.