Question

Three different objects of masses $m_1^{}$ , $m_2^{}$and $m_3^{}$ are allowed to fall from rest and from the same point '$O$' along three different frictionless paths. The speeds of the three objects on reaching the ground will be in the ratio of

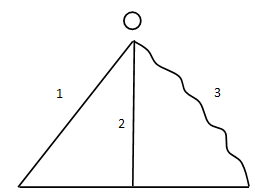
a.$m_1^{}:m_2^{}:m_3^{}$
b.$m_1^{}:2m_2^{}:m_3^{}$
c.$1:1:1$
d.$\dfrac{1}{{m_1^{}}}:\dfrac{1}{{m_2^{}}}:\dfrac{1}{{m_3^{}}}$

Answer 1

In question, they have asked about the speed of masses on reaching the ground, and given that bodies are at rest, and the path which they follow is a frictionless path. It simply implies that the question is related not to the kinetic energy of the body but the potential energy of bodies as they are at rest.
Formula Used:
$v = \sqrt {2gh}$
Where $v$ is the speed of an object, $g$ is the gravitational force, and $h$ is the height from the point at which the object is released

Complete Answer :
The kinematic equation for an object’s speed falling from rest to just before hitting the ground is given as
$v_{}^2 = 2gh$
$v = \sqrt {2gh}$
Three objects of different masses $m_1^{}$ , $m_2^{}$and $m_3^{}$fall from a point $O$. But according to the concept of potential energy, the speed $v$ will be the same as it does not depend on the path taken or the angle of inclination.
From the above equation, we get,
$v_1^{} = \sqrt {2gh}$
$v_2^{} = \sqrt {2gh}$
$v_3^{} = \sqrt {2gh}$
where $v_1^{},v_2^{},v_3^{}$ is the speed of masses $m_1^{}$ , $m_2^{}$ and $m_3^{}$ respectively, and $g$,$h$ is constant for all three objects.
Taking the ratio of $v_1^{}:v_2^{}$,
$v_1^{}:{v_2} = \dfrac{{v_1^{}}}{{v_2^{}}} = \dfrac{{\sqrt {2gh} }}{{\sqrt {2gh} }}$
$v_1^{}:{v_2} = 1:1$
Similarly for $v_2^{}$ and $v_3^{}$,
$v_2^{}:v_3^{} = 1:1$
We know that,
$a:b = p:q$
$b:c = q:r$
$a:b:c = p:q:r$
From the above equations, we get,
$v_1^{}:v_2^{}:v_3^{} = 1:1:1$

Hence the correct option is c) $1:1:1$

Note:
The equation $v_{}^2 = 2gh$ can be written as $\dfrac{1}{2}mv_{}^2 = mgh$ implies that the potential energy of an object from height h when released converts to the kinetic energy of the object when it reaches the ground
S.I unit of potential energy is the joule (J) and its dimensions are $[M_{}^{}L_{}^2T_{}^{ - 2}]$.
Work done by conservative forces depends only on initial and final positions. If it depended on velocity or path taken then forces would be non-conservative.