Question
Question: Three different dielectrics are filled in a parallel plate capacitor as shown. What should be the di...
Three different dielectrics are filled in a parallel plate capacitor as shown. What should be the dielectric constant of a material, which when fully filled between the plates produces the same capacitance?
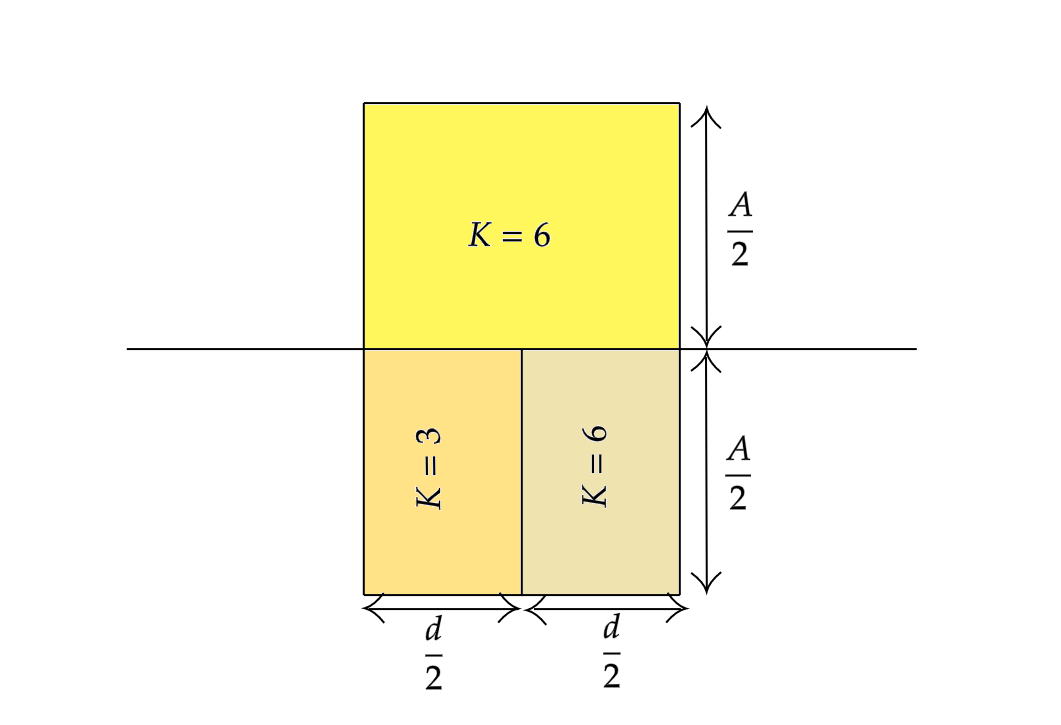
(A)4
(B)6
(C)5
(D)9
Solution
Whenever a dielectric is inserted between a parallel plate of a capacitor then the new value of the capacitor increases by k time the original capacitor. And if more than one dietetic material is inserted in between the parallel plated then each medium will act as a separate capacitor. Now using this concept first convert each dielectric into a separate capacitor so as to analyze their connection that they are in series or parallel. Now find the equivalent capacitor of the three dielectric materials and equate it with the original capacitance.
Complete answer:
We know that capacitance of a capacitor is given by,
C=dε0A
Where,
A is the area between the two parallel plates.
Distance between the two parallel plates is represented as d.
And ε0 is the permittivity of the space between the two parallel plates.
This is the case when it is between the two parallel plates.
But in this case three dielectric constants are inserted and in total let the dielectric constant be K which is always greater than one.
Therefore the new capacitance will become,
C′=dKε0A
Which is K time greater C .
Now from the above figure we can divide the capacitor into three different capacitors having different dielectric constant.
Case i:
K=3
C3=2d3ε02A
Now on simplifying we will get,
C3=d3ε0A
Case II:
In series with K=3
K=6
C6=2d6ε02A
Now on simplifying we will get,
C6=d6ε0A
Case III:
In parallel with K=3 and K=6
K=6
C6=d6ε02A
Now on simplifying we will get,
C6=d3ε0A
Now we can draw,
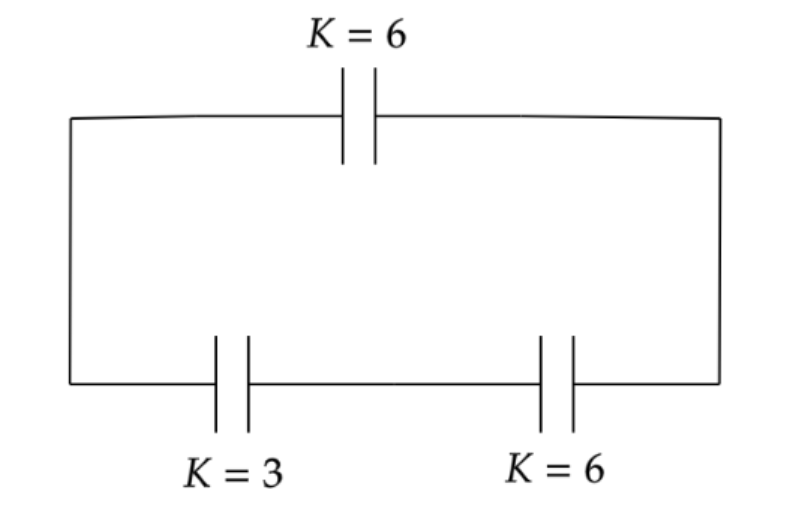
Now the equivalent capacitance from the above diagram will be,
Ceq=C6∣∣C3+C6(C3×C6)
Putting the values we will get,
Ceq=d3ε0A∣∣d3ε0A+d6ε0A(d3ε0A×d6ε0A)
Cancelling the common terms qe will get,
Ceq=d3ε0A∣∣9(d18ε0A)
Parallel capacitance are added,
Ceq=d3ε0A+d2ε0A
⇒Ceq=d5ε0A
As per the problem now equating this equivalent capacitance with C′ we will get,
C′=Ceq
Putting the respective values we will get,
dKε0A=d5ε0A
Cancelling the given terms we will get,
K=5
Therefore the correct option is (C) .
Note:
Remember that different materials have different dielectric constants like a perfectly conducting material has a dielectric constant of infinity while a perfectly insulating parallel has dielectric constant as zero. And note that while solving this type of problem first convert the dielectric into a separate category to solve the problem easily.
