Question
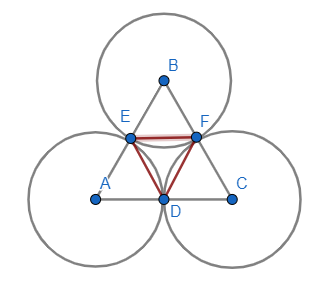
Question: Three congruent circles with centres A, B and C with radius 5cm each, touch each other at D, E and F...
Three congruent circles with centres A, B and C with radius 5cm each, touch each other at D, E and F as shown in the figure.
What is the perimeter of ΔABC ?
What is the length of DE of ΔDEF ?
 .
.
Solution
Hint: Notice that AE, EB, BF, FC, CD, and DA are equal to the radius of the congruent circles and radius is mentioned in the question. Use the mid-point theorem of a triangle to find the length of DE.
Complete step-by-step answer:
From the figure we can see that AE, EB, BF, FC, CD, and DA are equal to the radius of the congruent circles, and the radius is given as 5cm.
Now using the theorem above data to calculate the perimeter of the triangle.
Perimeter = AB + BC + CA
⇒ Perimeter = AE + EB + BF + FC + CD + DA =5+5+5+5+5+5=30cm.
Therefore, the perimeter of the triangle is 30cm.
Now moving on to find the length of DE. As AD = CD, we can say D is the midpoint of AC. Also, as AE=BE, we can say that E is the midpoint of AB.
According to the mid-point theorem, if a line joins the mid-points of the 2 sides of a triangle, then the line is parallel to the third side, and the length of the line is half the third side of the triangle.
∴DE=21BC=BF=FC=5=5
Therefore, the length of DE is 5cm.
Note: It is prescribed to learn all the basic theorems related to circles as they are regularly used in the questions related to circles and triangles, as we did in the above question. Also, learn all the properties related to different types of triangles as well.
