Question

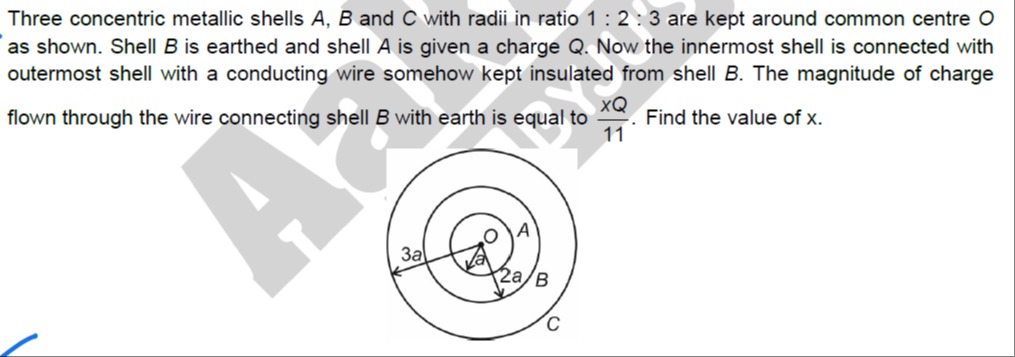
Three concentric metallic shells A, B and C with radii in ratio 1 : 2 : 3 are kept around common centre O as shown. Shell B is earthed and shell A is given a charge Q. Now the innermost shell is connected with outermost shell with a conducting wire somehow kept insulated from shell B. The magnitude of charge flown through the wire connecting shell B with earth is equal to $\frac{xQ}{11}$. Find the value of x.

Answer 1

3

Answer 2

The radii of the three concentric metallic shells A, B, and C are $R_A = a$, $R_B = 2a$, and $R_C = 3a$.

Initially, shell B is earthed, and shell A is given a charge Q. Shell C is initially uncharged.

In the initial state, let the charges on A, B, and C be $Q_A = Q$, $Q_B$, and $Q_C = 0$.

Since shell B is earthed, its potential $V_B = 0$.

The potential at $r=R_B=2a$ is $V_B = \frac{kQ_A}{R_B} + \frac{kQ_B}{R_B} + \frac{kQ_C}{R_C} = \frac{kQ}{2a} + \frac{kQ_B}{2a} + \frac{k(0)}{3a} = 0$.

This gives $\frac{Q}{2a} + \frac{Q_B}{2a} = 0$, so $Q_B = -Q$.

The initial charges are $Q_A = Q$, $Q_B = -Q$, $Q_C = 0$.

Now, the innermost shell A is connected with the outermost shell C with a conducting wire, insulated from shell B. Shell B remains earthed.

Let the final charges on A, B, and C be $Q'_A$, $Q'_B$, and $Q'_C$.

Since A and C are connected, they are at the same potential, $V_A = V_C$.

Shell B is earthed, so $V_B = 0$.

The combined system of A and C is isolated from the earth, so the total charge on A and C is conserved.

$Q'_A + Q'_C = Q_A + Q_C = Q + 0 = Q$.

The potentials at the surfaces of the shells are:

$V_A = \frac{kQ'_A}{R_A} + \frac{kQ'_B}{R_B} + \frac{kQ'_C}{R_C} = \frac{kQ'_A}{a} + \frac{kQ'_B}{2a} + \frac{kQ'_C}{3a}$

$V_B = \frac{kQ'_A}{R_B} + \frac{kQ'_B}{R_B} + \frac{kQ'_C}{R_C} = \frac{kQ'_A}{2a} + \frac{kQ'_B}{2a} + \frac{kQ'_C}{3a}$

$V_C = \frac{k(Q'_A + Q'_B + Q'_C)}{R_C} = \frac{k(Q'_A + Q'_B + Q'_C)}{3a}$

From $V_B = 0$:

$\frac{kQ'_A}{2a} + \frac{kQ'_B}{2a} + \frac{kQ'_C}{3a} = 0$

$3Q'_A + 3Q'_B + 2Q'_C = 0$ (Equation 1)

From $V_A = V_C$:

$\frac{kQ'_A}{a} + \frac{kQ'_B}{2a} + \frac{kQ'_C}{3a} = \frac{k(Q'_A + Q'_B + Q'_C)}{3a}$

Multiply by $\frac{3a}{k}$:

$3Q'_A + \frac{3}{2}Q'_B + Q'_C = Q'_A + Q'_B + Q'_C$

$3Q'_A + \frac{3}{2}Q'_B = Q'_A + Q'_B$

$2Q'_A = Q'_B - \frac{3}{2}Q'_B = -\frac{1}{2}Q'_B$

$4Q'_A = -Q'_B$ (Equation 2)

From conservation of charge on A and C:

$Q'_A + Q'_C = Q$ (Equation 3)

Now solve the system of equations.

Substitute $Q'_B = -4Q'_A$ from Equation 2 into Equation 1:

$3Q'_A + 3(-4Q'_A) + 2Q'_C = 0$

$3Q'_A - 12Q'_A + 2Q'_C = 0$

$-9Q'_A + 2Q'_C = 0$ (Equation 4)

From Equation 3, $Q'_C = Q - Q'_A$. Substitute this into Equation 4:

$-9Q'_A + 2(Q - Q'_A) = 0$

$-9Q'_A + 2Q - 2Q'_A = 0$

$-11Q'_A + 2Q = 0$

$11Q'_A = 2Q$

$Q'_A = \frac{2Q}{11}$.

Now find $Q'_B$:

$Q'_B = -4Q'_A = -4 \left(\frac{2Q}{11}\right) = -\frac{8Q}{11}$.

The charge flown through the wire connecting shell B with earth is the change in charge on shell B, which came from or went to the earth.

Initial charge on B was $Q_B = -Q$.

Final charge on B is $Q'_B = -\frac{8Q}{11}$.

The charge that flowed onto shell B is $Q'_B - Q_B = -\frac{8Q}{11} - (-Q) = -\frac{8Q}{11} + Q = \frac{-8Q + 11Q}{11} = \frac{3Q}{11}$.

This means a charge of $\frac{3Q}{11}$ has flowed from the earth to shell B.

The magnitude of the charge flown through the wire connecting shell B with earth is $\left|\frac{3Q}{11}\right| = \frac{3|Q|}{11}$.

The problem states that the magnitude of charge flown is $\frac{xQ}{11}$. Assuming Q is a positive quantity in this context (as the result is given in terms of Q), we have:

$\frac{3Q}{11} = \frac{xQ}{11}$

$3 = x$.