Question

Three concentric circles of which the biggest is ${x^2} + {y^2} = 1$ have their radii in A.P. with common difference $d( > 0)$ . If the line $y = x + 1$ cuts all the circles in real distinct points, then
a.$d < \dfrac{{2 - \sqrt 2 }}{4}$
b.$d > \dfrac{{2 + \sqrt 2 }}{4}$
c.$d > 1 + \dfrac{1}{{\sqrt 2 }}$
d.$d$ is any real number

Answer 1

Concentric circles are those circles that have the same center but different radii. The equation of a circle having a center at the origin and radius $r$ units is given by ${x^2} + {y^2} = {r^2}$ . A sequence of numbers is considered to be in arithmetic progression(A.P.) if the difference between the numbers is constant.
FORMULA:
The distance of a point $({x_1},{y_1})$ from the line $ax + by + c = 0$ is given by $\dfrac{{|ax + by + c|}}{{\sqrt {{a^2} + {b^2}} }}$ .

Complete answer:
First, we calculate the radius of the biggest circle ${x^2} + {y^2} = 1$ .
The equation of the circle is of the form ${x^2} + {y^2} = {r^2}$ where the origin is $(0,0)$ and radius is $r$ units.
The circle has its center at the origin i.e. $(0,0)$ and radius is $1$ unit.
Therefore, the other two circles will also have their centers at origin i.e. $(0,0)$ because they are concentric circles.
Let the radii of the other two concentric circles be ${r_1}$ and ${r_2}$ .
The radii of the three concentric circles are in A.P. where $1 > {r_2} > {r_1}$ .
The common difference between the consecutive radii is $d > 0$ .
$\therefore {r_2} = 1 - d$ and ${r_1} = 1 - 2d$ .

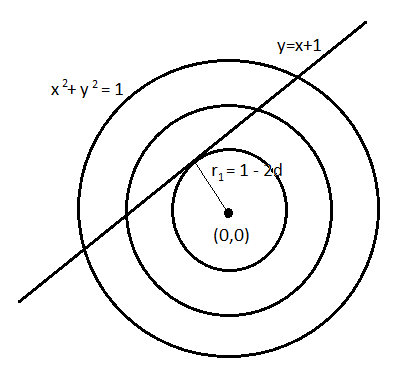
The line $y = x + 1$ cuts all three circles into real distinct points.
$\therefore$ Distance from the origin i.e. $(0,0)$ to the line $y = x + 1$ is given by
$= \dfrac{{|1 \times 0 - 1 \times 0 + 1|}}{{\sqrt {{1^2} + {1^2}} }}$
$= \dfrac{1}{{\sqrt 2 }}$
Therefore the radius of the smallest circle will be greater than the distance of the line from the origin.
This is because if the distance is greater from the origin then the line will not cut the circle into real distinct points and if the distance is equal to the radius then the line will be a tangent to the circle which will not cut the circle in real distinct points.
$\therefore {r_1} > \dfrac{1}{{\sqrt 2 }}$
Again, ${r_1} = 1 - 2d$ therefore we substitute ${r_1}$ in the above relation and we get:
$1 - 2d > \dfrac{1}{{\sqrt 2 }}$
$\Rightarrow - 2d > \dfrac{1}{{\sqrt 2 }} - 1$
$\Rightarrow - 2d > \dfrac{{1 - \sqrt 2 }}{{\sqrt 2 }}$
$\Rightarrow - d > \dfrac{{ - (\sqrt 2 - 1)}}{{2\sqrt 2 }}$
$\Rightarrow d < \dfrac{{(\sqrt 2 - 1)}}{{2\sqrt 2 }}$
Multiplying both numerator and denominator on the R.H.S. with $\sqrt 2$ we get:
$d < \dfrac{{(\sqrt 2 - 1)}}{{2\sqrt 2 }}$
$\Rightarrow d < \dfrac{{\sqrt 2 \times (\sqrt 2 - 1)}}{{\sqrt 2 \times 2\sqrt 2 }}$
$\Rightarrow d < \dfrac{{(2 - \sqrt 2 )}}{4}$

Hence the correct option is (A) $d < \dfrac{{(2 - \sqrt 2 )}}{4}$ .

Note:
If the line does not cut the circles in distinct points then the distance from the origin to the line may have been equal to the radius. In that case, the line would have been a tangent to the circle. Since the circles are concentric so they have the same center. The distance from the center can never be greater than the radius of the circle. Then the line would lie outside the circle.