Question
Question: Three circles of radii \[r\], \[2r\], and \[r\] are drawn with their centres on the diagonal of a sq...
Three circles of radii r, 2r, and r are drawn with their centres on the diagonal of a square, touching one another and the square as shown. What is the ratio of the
radius of the smaller circles to the side of the square?
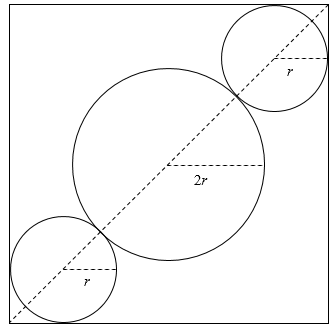
Solution
Here, we need to find the ratio of the radius of the smaller circle and the side of the square. We will first construct the perpendiculars and use the properties of a square to find the measure of the angles. We will then use the trigonometric ratio of tangent to find the length of the diagonal in terms of the radius of the smaller circle. Then, we will use Pythagoras’s theorem to find the required ratio of the radius of the smaller circle and the side of the square.
Complete step-by-step answer:
First, we will mark the points and construct perpendiculars in the diagram.
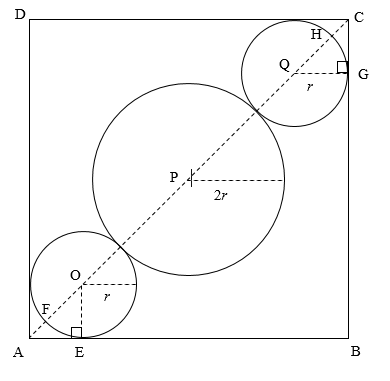
Here, ABCD is the square, and OE is perpendicular to AB, and QG is perpendicular to BC.
OE, OF, QG, and QH are the radii of the smaller circles.
Thus, we get
OE=OF=QG=QH=r
AC is the diagonal of square ABCD.
We know that each interior angle of a square is a right angle.
Therefore, we get
∠DAB=∠BCD=90∘
The diagonal of a square bisect the interior angles.
Therefore, we get
∠CAB=21∠DAB=21×90∘=45∘
∠ACB=21∠BCD=21×90∘=45∘
Thus, we get
∠OAE=∠CAB=45∘
∠QCG=∠ACB=45∘
We can observe that the triangle OAE is a right angled triangle.
The tangent of an angle θ in a right angled triangle is given by tanθ=BasePerpendicular.
Therefore, in triangle OAE, we get
tan45∘=AEOE
Substituting tan45∘=1 in the equation, we get
⇒1=AEOE ⇒OE=AE
Thus, we get
⇒OE=AE=r
We will use the Pythagoras’s theorem in the right angled triangle OAE.
In triangle OAE, OA is the hypotenuse, AE is the base, and OE is the height.
Therefore, in triangle OAE, we get
OA2=AE2+OE2
The side OA is the sum of the lengths AF and FO.
Substituting OA=AF+OF and OE=AE=r in the equation, we get
⇒(AF+OF)2=r2+r2
Substituting OF=r in the equation, we get
⇒(AF+r)2=2r2
Taking the square root of both sides, we get
⇒AF+r=2r
Thus, we get
⇒AF=2r−r ⇒AF=r(2−1)
Similarly, using the triangle QCG, we get CH=r(2−1).
The diagonal AC is the sum of the lengths AF, CH, and the diameters of the three circles.
Therefore, we get
⇒AC=r(2−1)+2r+2(2r)+2r+r(2−1)
Simplifying the expression, we get
⇒AC=r(2−1)+2r+4r+2r+r(2−1) ⇒AC=2r−r+2r+4r+2r+2r−r
Adding and subtracting the like terms, we get
⇒AC=22r+6r ⇒AC=r(22+6)
Now, we can observe that triangle ABC is a right angled triangle because the interior angles of a square are right angles.
Let the sides AB, BC, CD, and AD of the square be of length x.
Thus, using the Pythagoras’s theorem in triangle ABC, we get
AC2=AB2+BC2
Substituting AB=BC=x and AC=r(22+6) in the equation, we get
⇒(r(22+6))2=x2+x2
Simplifying the expression, we get
⇒r2(22+6)2=2x2
Taking the square root of both sides, we get
⇒r(22+6)=2x
Dividing both sides of the equation by x(22+6), we get
⇒x(22+6)r(22+6)=x(22+6)2x ⇒xr=22+62
We get the ratio of the radius of the smaller circles and the side of the square as 22+62.
Note: We used the Pythagoras’s theorem in the solution. The Pythagoras’s theorem states that the square of the hypotenuse of a right angled triangle is equal to the sum of squares of the other two sides, that is Hypotenuse2=Base2+Perpendicular2. The hypotenuse of a right angled triangle is its longest side. Pythagora's theorem can be used only in right angled triangles. For other types of triangles, we use Heron’s formula.
