Question
Question: Three circles each of radius r units are drawn inside an equilateral triangle of side ‘a’ units, suc...
Three circles each of radius r units are drawn inside an equilateral triangle of side ‘a’ units, such that each circle touches the other two and two sides of the triangle as shown in the figure, (P, Q and R are the centres of the three circles). Then the relation between r and a is
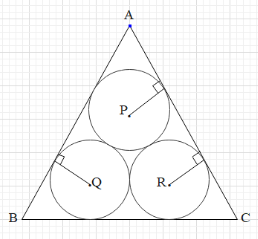
A. a=2(3+1)r
B. a=(3+1)r
C. a=(3+2)r
D. a=2(3+2)r
Solution
To solve the given question, we must have the knowledge of trigonometry, rules of congruence and properties of a triangle and a rectangle. Divide the given figure into known shapes. Then find the value of one of the sides in terms of the radius of the circle.
Complete step by step answer:
We know that in an equilateral triangle all the sides are of equal lengths and the angles are of 60∘ each. Let us draw some line segments and shown below.

In this, the quadrilateral QRYX is a rectangle since all angles are right angles.
Also we can see that QR=2r.
The opposite sides of a rectangle are equal. Then this means that QR=XY=2r.
Now consider ΔBTQ and ΔBXQ. Here,
TQ=XQ=r, since they both are the radius of the circle.
∠BTQ=∠BXQ=90∘.
And the two triangles have a common side BQ.
With this, we get that ΔBTQ≅ΔBXQ, by RHS congruence rule.
Now, since ΔBTQ≅ΔBXQ, ∠TBQ=∠XBQ.
But ∠TBQ+∠XBQ=∠TBX=60∘
Substitute ∠TBQ=∠XBQ.
⇒∠XBQ+∠XBQ=60∘
⇒∠XBQ=30∘ ⇒∠XBQ=30∘.
From the knowledge of trigonometry we get that in ΔBXQ, tan30∘=BXQX=BXr.
And tan30∘=31
⇒tan30∘=31=BXr
⇒BX=3r.
Similarly, we will get that YC=3r
And from the figure, a=BX+XY+YC .
Substitute the values of BX, XY and YC.
⇒a=3r+2r+3r
∴a=2(3+1)r
Therefore, we found a relation between a and r. Hence, the correct option is A.
Note: We can see that the given figure has multiple lines of symmetry. Therefore, we do not have to really prove that ΔBTQ≅ΔBXQ. Due to symmetry the two triangles will be congruent. Hence, without wasting any time we can write that ∠TBQ=∠XBQ. This will help in competitive exams.
