Solveeit Logo
Login

Question

Question: Three charges \( - \sqrt 2 \mu C,2\sqrt 2 \mu C\)and \( - \sqrt 2 \mu C\) are arranged as shown. Tot...

Three charges −2μC,22μC - \sqrt 2 \mu C,2\sqrt 2 \mu Cand −2μC - \sqrt 2 \mu C are arranged as shown. Total electric field intensity at P is:

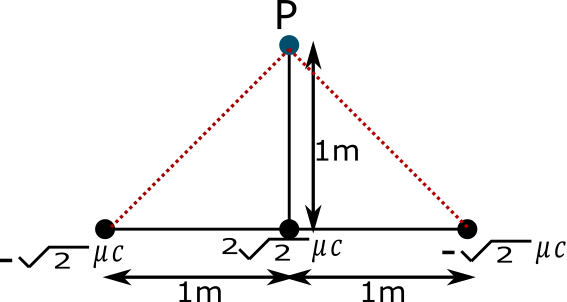
A) 18×103N/C18 \times {10^3}N/C
B) (22−1)×9×103N/C\left( {2\sqrt 2 - 1} \right) \times 9 \times {10^3}N/C
C) Zero
D) (22+1)×9×103N/C\left( {2\sqrt 2 + 1} \right) \times 9 \times {10^3}N/C

Explanation

Solution

We simply apply here formula for electric field intensity at a point due to a point charge. Here in question three charges are given so we find three electric field intensity on point P. To find the net electric field on point P can be calculated by vector addition of all three electric fields.

Complete step by step solution:
Step 1
First we draw diagram mark electric field direction due to all three charges

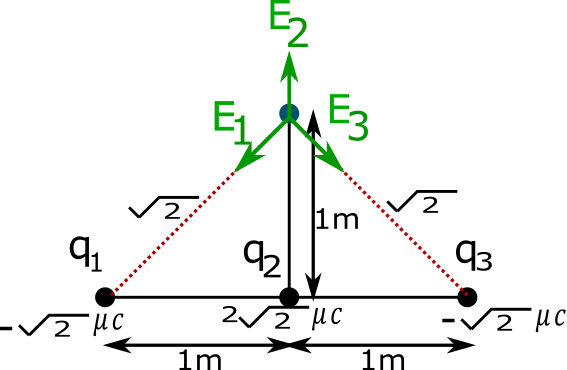
Here charge q1=−2μC,q2=22μC{q_1} = - \sqrt 2 \mu C,{q_2} = 2\sqrt 2 \mu C and q3=−2μC{q_3} = - \sqrt 2 \mu C
Electric field due to charge q1{q_1} is E1{E_1} toward charge because of negative charge
Electric field due to charge q2{q_2} is E2{E_2} away from q2{q_2} because of positive charge
Electric field due to q3{q_3} is E3{E_3} toward q3{q_3} because of negative charge
Electric field at a point due to a point charge is given by E=kqr2E = \dfrac{{kq}}{{{r^2}}}
Here E is the electric field
k is a constant k=9×109k = 9 \times {10^9}
rr Is the distance between charge and point
Calculate E1{E_1}
⇒E1=kq1r2\Rightarrow {E_1} = \dfrac{{k{q_1}}}{{{r^2}}}
Here r=2r = \sqrt 2 from figure
⇒E1=k2×10−6C(2)2\Rightarrow {E_1} = \dfrac{{k\sqrt 2 \times {{10}^{ - 6}}C}}{{{{\left( {\sqrt 2 } \right)}^2}}}
⇒E1=k×10−62N/C\Rightarrow {E_1} = \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}N/C At 45∘{45^\circ } from negative y-axis toward negative x-axis
Electric field due to q2{q_2}
⇒E2=kq2r2\Rightarrow {E_2} = \dfrac{{k{q_2}}}{{{r^2}}}
Here r=1mr = 1m given in question
⇒E2=k×22×10−61\Rightarrow {E_2} = \dfrac{{k \times 2\sqrt 2 \times {{10}^{ - 6}}}}{1}
⇒E2=k(22×10−6)N/C\Rightarrow {E_2} = k\left( {2\sqrt 2 \times {{10}^{ - 6}}} \right)N/C Toward positive y- axis direction
Now E3{E_3}
⇒E3=kq3r2\Rightarrow {E_3} = \dfrac{{k{q_3}}}{{{r^2}}}
Here r=2mr = \sqrt 2 m from diagram
⇒E3=k×2×10−6(2)2\Rightarrow {E_3} = \dfrac{{k \times \sqrt 2 \times {{10}^{ - 6}}}}{{{{\left( {\sqrt 2 } \right)}^2}}}
⇒E3=k×10−62N/C\Rightarrow {E_3} = \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}N/C At 45∘{45^\circ } from negative y-axis toward positive x- axis.

Step 2
We assume net electric field due to all three charges is EE then
⇒E→=E→1+E→2+E→3\Rightarrow \overrightarrow E = {\overrightarrow E _1} + {\overrightarrow E _2} + {\overrightarrow E _3}
We make diagram for E1,E2{E_1},{E_2} and E3{E_3} with x-y axis

X component for net electric field Ex{E_x}
⇒Ex=E1x+E2x+E3x\Rightarrow {E_x} = {E_{1x}} + {E_{2x}} + {E_{3x}}
⇒Ex=−k×10−62sin⁡45+0+k×10−62sin⁡45\Rightarrow {E_x} = - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\sin 45 + 0 + \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\sin 45
Solving this
∴Ex=0\therefore {E_x} = 0
Y component of net electric field Ey{E_y}
⇒Ey=E1y+E2y+E3y\Rightarrow {E_y} = {E_{1y}} + {E_{2y}} + {E_{3y}}
⇒Ey=(−k×10−62cos⁡45)+(k(22×10−6))+(−k×10−62cos⁡45)\Rightarrow {E_y} = \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\cos 45} \right) + \left( {k\left( {2\sqrt 2 \times {{10}^{ - 6}}} \right)} \right) + \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\cos 45} \right)
⇒Ey=(−k×10−62×12)+(k×22×10−6)+(−k×10−62×12)\Rightarrow {E_y} = \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }} \times \dfrac{1}{{\sqrt 2 }}} \right) + \left( {k \times 2\sqrt 2 \times {{10}^{ - 6}}} \right) + \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }} \times \dfrac{1}{{\sqrt 2 }}} \right)
Solving this
⇒Ey=(k×10−6)(−12+22−12)\Rightarrow {E_y} = \left( {k \times {{10}^{ - 6}}} \right)\left( { - \dfrac{1}{2} + 2\sqrt 2 - \dfrac{1}{2}} \right)
⇒Ey=(k×10−6)(22−1)\Rightarrow {E_y} = \left( {k \times {{10}^{ - 6}}} \right)\left( {2\sqrt 2 - 1} \right)
Put the value of constant k
k=9×109k = 9 \times {10^9}
⇒Ey=(9×109×10−6)(22−1)\Rightarrow {E_y} = \left( {9 \times {{10}^9} \times {{10}^{ - 6}}} \right)\left( {2\sqrt 2 - 1} \right)
Solving again
⇒Ey=(22−1)(9×103)N/C\Rightarrow {E_y} = \left( {2\sqrt 2 - 1} \right)\left( {9 \times {{10}^3}} \right)N/C
So net electric field
⇒E=(Ex)2+(Ey)2\Rightarrow E = \sqrt {{{\left( {{E_x}} \right)}^2} + {{\left( {{E_y}} \right)}^2}}
⇒E=(0)2+[(22−1)(9×103)]2\Rightarrow E = \sqrt {{{\left( 0 \right)}^2} + {{\left[ {\left( {2\sqrt 2 - 1} \right)\left( {9 \times {{10}^3}} \right)} \right]}^2}}
Hence
∴E=(22−1)(9×103)N/C\therefore E = \left( {2\sqrt 2 - 1} \right)\left( {9 \times {{10}^3}} \right)N/C
So we find net electric field (22−1)×9×103N/C\left( {2\sqrt 2 - 1} \right) \times 9 \times {10^3}N/C

Hence option B is correct

Note: In the question we take direction of electric field in positive charge away from the charge and in case of negative charge take toward the charge reason is electric field line
In positive charge electric field lines go away from the positive charge means appears to emit from positive charge and field lines appear to converse at negative charge. So we take the field direction according to this assumption.