Question

Three charges - q, Q and - q are placed at equal distances on a straight line. If the total potential energy of the system of three charges is zero, then the ratio Q: q is
(A) 1:2
(B) 2:1
(C) 1:1
(D) 1:4

Answer 1

In this question, we need to determine the ratio of the two charges Q and q such that - q, Q and - q are placed at equal distances on a straight line. For this, we will use a potential energy formula for the electrostatic system and put it equal to zero, and solve for Q:q.

Complete step by step answer:
The potential energy between the charged particles is given as,
$U = K\dfrac{{{Q_1}{Q_2}}}{d}$ where, $K = \dfrac{1}{{4\pi {\varepsilon _0}}}$.
The following figure depicts the pictorial representation of the placement of the charged particles.

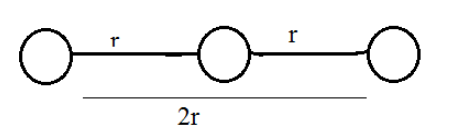
Net U= potential energy due to -q and Q + potential energy due to Q and - q + potential energy due to -q and -q
${U_{net}} = K\left( {\dfrac{{ - qQ}}{r}} \right) + K\left( {\dfrac{{ - qQ}}{r}} \right) + K\left( {\dfrac{{ - {q^2}}}{{2r}}} \right)$
According to the question, the net potential energy of the combination is zero. So,
${U_{net}} = 0 \\\ \Rightarrow K\left( {\dfrac{{ - qQ}}{r}} \right) + K\left( {\dfrac{{ - qQ}}{r}} \right) + K\left( {\dfrac{{ - {q^2}}}{{2r}}} \right) = 0 \\\ \Rightarrow\dfrac{{Kq}}{r}\left( { - Q - Q + \dfrac{q}{2}} \right) = 0 \\\ \Rightarrow - 2Q + \dfrac{q}{2} = 0 \\\ \Rightarrow - 2Q = - \dfrac{q}{2} \\\ \therefore\dfrac{Q}{q} = \dfrac{1}{4} \\\$
Hence, the ratio of the charge Q and q is 1:4.
Hence,option D is correct.

Note: Don’t forget to write the sign of the charge with its magnitude. The electric potential energy of a system of point charges is defined as the work required assembling the system of charges by bringing them close together, as in the system from an infinite distance.