Question

Three charges $- q$ , $Q$ , and $- q$ are placed at equal distances on a straight line. If the total potential energy of the system of three charges is zero then the ratio $Q:q$ is:
A) 1:2
B) 2:1
C) 1:1
D) 1:4

Answer 1

The electric potential energy of a system of point charges is defined as the work required to assemble this system of charges by bringing them close together, as in the system from an infinite distance. The electrostatic potential energy of a system containing only one point charge is zero, as there are no other sources of electrostatic force against which an external agent must do work in moving the point charge from infinity to its final location. Use the potential energy formula in which the potential energy is directly proportional to the multiplication of the number of charges and inversely proportional to the distance between the charges in a charging system of two charged particles.

Complete step by step solution:
Step 1: consider the following figure
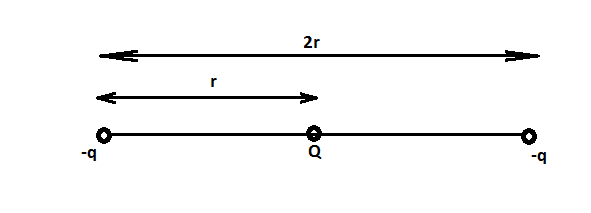Three charges are placed in a straight line. Now express the formula for the potential energy for the two charged particle system
$\therefore U = k\dfrac{{{q_1}{q_2}}}{r}$ , where $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$ is a constant, $r$ is the distance between two charged particles ${q_1}$ and ${q_2}$ .
Step 2: The potential energy of the system is given by $U = {U_{ - q,Q}} + {U_{ - q, - q}} + {U_{Q, - q}}$ . Now calculate each term on the right-hand side individually.
Step 3: The distance between $- q$ and $Q$ is $r$ therefore
$\therefore {U_{ - q,Q}} = k\dfrac{{ - qQ}}{r}$…..equation (1).
Similarly, for the $Q$ and $- q$ the potential difference will be
$\therefore {U_{Q, - q}} = k\dfrac{{ - qQ}}{r}$…..equation (2).
Now the distance between $- q$ and $- q$ is $2r$ , therefore, the potential energy will be
$\therefore {U_{ - q, - q}} = k\dfrac{{( - q)( - q)}}{{2r}}$…..equation (3).
Step 4: Now from the equation 1,2 and 3 we can have
$\therefore U = k\dfrac{{ - qQ}}{r} + k\dfrac{{ - qQ}}{r} + k\dfrac{{( - q)( - q)}}{{2r}}$
Take $\dfrac{k}{{2r}}$ as a common
$\therefore U = \dfrac{k}{{2r}}( - 2qQ - 2qQ + {q^2})$
$\Rightarrow U = \dfrac{k}{{2r}}( - 4qQ + {q^2})$
Step 5: But it is given that the potential energy of the system is zero. Therefore,
$\Rightarrow U = \dfrac{k}{{2r}}( - 4qQ + {q^2}) = 0$
It is clear that when two variables in multiplication equal zero then one of them or both are zero. But we can see above that $\dfrac{k}{{2r}}$ cannot be zero. Therefore,
$\therefore ( - 4qQ + {q^2}) = 0$
$\Rightarrow 4qQ = {q^2}$
$\Rightarrow 4Q = q$
$\Rightarrow \dfrac{Q}{q} = \dfrac{1}{4}$
Thus we have $Q:q = 1:4$ .

Hence the option D is correct.

Note: When the electric potential energy of a charged particle system is zero it means that the ability to do work of the system is zero. But it does not mean that the Coulomb forces between the charges are zero. The sign taken of the charges depends on the nature of the charge. Because the nature of charge causes the attractive or repulsive force between two charges which is responsible for the electric potential energy of the entire system.