Question

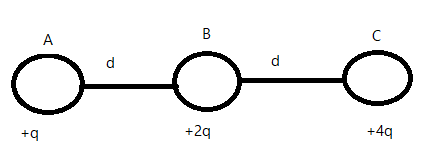
Three charges $+q$, $+2q$ and $+4q$ are connected by strings as shown in the figure. What is the ratio of tension in the strings AB and BC?

& A.1:2 \\\ & B.1:3 \\\ & C.2:1 \\\ & D.3:1 \\\ \end{aligned}$$

Answer 1

Consider the given diagram in the question as a system. Then are two forces that act on the system. One is the tension on the string, and the other is the electric force exerted by the charges. We know that the electric force between the charges is given by Coulomb's law.

Formula used:
$F=k\dfrac{q_{1}q_{2}}{r^{2}}$

Complete step-by-step answer:
We know that the electric force experienced due to a pair charges is given by Coulomb's force. Clearly, the electric force depends on the charge q and inversely proportional to the square of the distance between them.
We know that, the electrical force $F$ between two charges $q_{1}$ and $q_{2}$ which is separated at a distance $r$ is given as $F=k\dfrac{q_{1}q_{2}}{r^{2}}$,where $k=\dfrac{1}{4\pi\epsilon_{0}}$ which is constant with a value $9\times 10^{9}$.
Here we have three positive charges, $q_{1}=+q$, $q_{2}=+2q$ and $q_{3}=+4q$ which are a distance $r=d$ from each other as shown below:

Let us assume that the system is in equilibrium. Then we can say that the tension on charge A $T_{AB}$ is equal to the electrical force on the charge A $E_{A}$.
$\implies T_{AB}=E_{A}$
Then the electrical force on the charge A $E_{A}$, is given as $E_{A}=k\left[\dfrac{2q^{2}}{d^{2}}+\dfrac{4q^{2}}{4d^{2}}\right]=\dfrac{3kq^{2}}{d^{2}}$
$\implies T_{AB}=\dfrac{3kq^{2}}{d^{2}}$
Similarly, we can say that the tension on charge C $T_{BC}$ is equal to the electrical force on the charge C $E_{C}$.
$\implies T_{BC}=E_{C}$
Then the electrical force on the charge C $E_{C}$, is given as $E_{C}=k\left[\dfrac{8q^{2}}{d^{2}}+\dfrac{4q^{2}}{4d^{2}}\right]=\dfrac{9kq^{2}}{d^{2}}$
$\implies T_{BC}=\dfrac{9kq^{2}}{d^{2}}$
Taking the ratio, we get, $\dfrac{T_{AB}}{T_{BC}}=\dfrac{\dfrac{9kq^{2}}{d^{2}}}{\dfrac{3kq^{2}}{d^{2}}}=\dfrac{1}{3}$
Hence the answer is $B.1:3$

So, the correct answer is “Option B”.

Note: We know that the electric force due to a pair of charges is given by Coulomb's law. This force can be attractive or repelling depending on the nature of the charges. An electric field can be produced by a time-varying electric field or an electrical charge. These can be either attracting or repelling in nature.