Question

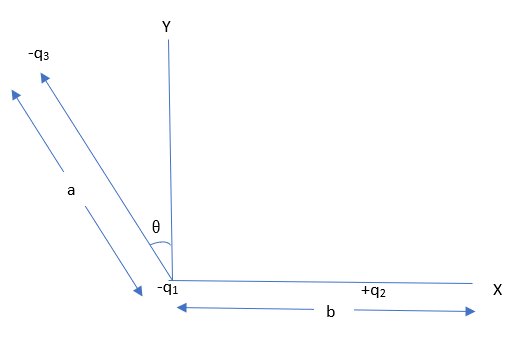
Three charges $- {q_1}$ , $+ {q_2}$ and $- {q_3}$ are placed as shown in the figure. The x-component of the force on $- {q_1}$ is proportional to:
$\left( {\text{A}} \right)\dfrac{{{q_2}}}{{{b^2}}} - \dfrac{{{q_3}}}{{{a^2}}}\cos \theta \\\ \left( {\text{B}} \right)\dfrac{{{q_2}}}{{{b^2}}} + \dfrac{{{q_3}}}{{{a^2}}}\sin \theta \\\ \left( {\text{C}} \right)\dfrac{{{q_2}}}{{{b^2}}} + \dfrac{{{q_3}}}{{{a^2}}}\cos \theta \\\ \left( {\text{D}} \right)\dfrac{{{q_2}}}{{{b^2}}} - \dfrac{{{q_3}}}{{{a^2}}}\sin \theta \\\$

Answer 1

Hint : Since we have been given three charges, first try to find the forces on charge ${q_1}$ due to the other two charges since we have to find the x-component of force on $- {q_1}$ . The force between two charges is to be found out by coulombs formula. After this step find out the x-component of the force.
${\text{F = k}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}$
Where F= electric force
k=Coulomb constant
${q_1},{q_2}$ = charges
r=distance of separation.

Complete Step By Step Answer:
we have been given three charges $- {q_1}$ , $+ {q_2}$ and $- {q_3}$ also we have been shown in the diagram about the placements of this charges. All we have to find is the x-component of the force $- {q_1}$ .
We all know that the charges present in the given position will have repulsive and attractive forces between each other. Hence $- {q_1}$ and $- {q_3}$ will repel each other and this two charges will attract $+ {q_2}$ .
hence we will try to calculate the force between these charges. Since we have to find the x-component of force on $- {q_1}$ , we will try to find the force on $- {q_1}$ due to $+ {q_2}$ and $- {q_3}$ .
We will use the formula ${\text{F = k}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}$
Where F= electric force
k=Coulomb constant
${q_1},{q_2}$ = charges
r=distance of separation.
Hence the force due to ${q_2}$ on ${q_1}$ is ${{\text{F}}_{12}}{\text{ = k}}\dfrac{{{q_1}{q_2}}}{{{b^2}}}$ as the distance between this two charges is b.
The force due to ${q_3}$ on ${q_1}$ is ${{\text{F}}_{13}}{\text{ = k}}\dfrac{{{q_1}{q_3}}}{{{a^2}}}$ as the distance between this two charges is a.
x-component of the force on ${q_1}$ will be ${F_{12}} + {F_{13}}\sin \theta$
hence ${F_x} = {\text{k}}\dfrac{{{q_1}{q_2}}}{{{b^2}}}{\text{ + k}}\dfrac{{{q_1}{q_3}}}{{{a^2}}}\sin \theta$
${F_x}$ $\alpha \dfrac{{{q_2}}}{{{b^2}}}{\text{ + }}\dfrac{{{q_3}}}{{{a^2}}}\sin \theta$
hence option (B) matches our solution.
Hence (B) $\dfrac{{{q_2}}}{{{b^2}}}{\text{ + }}\dfrac{{{q_3}}}{{{a^2}}}\sin \theta$ is the right answer.

Note :
While solving problems of this type, you should always draw a diagram indicating the forces on the charge. Also find out the directions of the vector by looking at the sign and draw in it the diagram. Since force is a vector, so when one or more charges exert pressure on the other, the net force on the charge is the vector sum of the individual forces.