Question

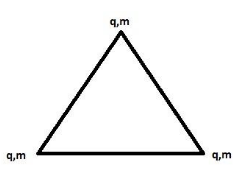
Three charges lie on the vertex of an equilateral triangle of side ‘ ’. The charges are initially at rest. They are allowed to move in gravity free space under the action of mutual repulsion. If $\left( {m = \dfrac{{k{q^2}}}{l}} \right)$ is the mass of particles then the speed of any of them when separation becomes $2l$ is (in m/s)?

Answer 1

Hint : We need to use the law of conservation of energy to solve this problem. By equating the total energy, which is the sum of the kinetic and the potential energy, for the initial and final cases, we will get the answer.

Formula Used: The formulae used in the solution are given here as,
$\Rightarrow {\left( {P.E. + K.E.} \right)_{initial}} = {\left( {P.E. + K.E.} \right)_{final}}$ where $K.E.$ and $P.E.$ are the kinetic energy and potential energy of a body respectively.
$\Rightarrow K.E. = \dfrac{1}{2}m{v^2}$ where $m$ is the mass and $v$ is the velocity of a body.
$\Rightarrow P.E. = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{r}$ where $Q$ and $q$ are two charges and $r$ is the closest distance of approach.

Complete step by step answer
Kinetic energy is the energy an object possesses because of its motion. This energy is dependent on the velocity of the object squared.
$\Rightarrow K.E. = \dfrac{1}{2}m{v^2}$ where $m$ is the mass and $v$ is the velocity of a body.
Potential energy is energy stored as the result of its position. The electric potential energy of any given system of charges is the work done by an external agent in bringing the charge from infinity to the present configuration in an electric field.
According to the law of conservation of energy, energy is neither created nor destroyed. It is only transformed from state to another.
Thus for the given system, it can be written that,
$\Rightarrow {\left( {P.E. + K.E.} \right)_{initial}} = {\left( {P.E. + K.E.} \right)_{final}}$ where $K.E.$ and $P.E.$ are the kinetic energy and potential energy of a body respectively.
Initially, the charges are at rest, thus $K.E{._{initial}} = 0$ .
$\Rightarrow {\left( {P.E. + K.E.} \right)_{initial}} = {U_i} + 0$
Initial Electrostatic Potential Energy is given by the formula $P.E. = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{r} = \dfrac{{k{q^2}}}{l}$
Hence total potential energy,
$\therefore {U_i} = \dfrac{{k{q^2}}}{l} + \dfrac{{k{q^2}}}{l} + \dfrac{{k{q^2}}}{l}$
$\Rightarrow {U_i} = \dfrac{{3k{q^2}}}{l}$ .
So the total initial energy is,
$\Rightarrow {\left( {P.E. + K.E.} \right)_{initial}} = \dfrac{{3k{q^2}}}{l}$
At the final stage, the potential energy will be, ${U_f} = \dfrac{{3k{q^2}}}{{2l}}$
So the total energy is,
$\Rightarrow {\left( {P.E. + K.E.} \right)_{final}} = \dfrac{{3k{q^2}}}{{2l}} + {K_f}$
Here the final kinetic energy will be,
$\Rightarrow {K_f} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}m{v^2} + \dfrac{1}{2}m{v^2}$
$\Rightarrow {K_f} = \dfrac{3}{2}m{v^2}$
$\therefore {\left( {P.E. + K.E.} \right)_{final}} = \dfrac{{3k{q^2}}}{{2l}} + \dfrac{3}{2}m{v^2}$
By law of conservation of energy, ${\left( {P.E. + K.E.} \right)_{initial}} = {\left( {P.E. + K.E.} \right)_{final}}$
By substituting we get,
$\Rightarrow \dfrac{{3k{q^2}}}{l} = \dfrac{{3k{q^2}}}{{2l}} + \dfrac{3}{2}m{v^2}$
So we get,
$\Rightarrow \dfrac{{3k{q^2}}}{{2l}} = \dfrac{3}{2}m{v^2}$
Cancelling the similar terms,
$\Rightarrow \dfrac{{k{q^2}}}{{ml}} = {v^2}$
Since the mass is given as $\left( {m = \dfrac{{k{q^2}}}{l}} \right)$
$\Rightarrow v = \sqrt {\dfrac{{k{q^2}l}}{{k{q^2}l}}}$
Thus, the velocity of the particles is,
$v = 1m/s$ .

Note
Electric potential energy is defined as the total potential energy a unit charge will possess if located at any point in the outer space. It is the total work done by an external agent in bringing the charge or the system of charges from infinity to the present configuration without undergoing any acceleration.