Question

Three charges each of value q are placed at the corners of an equilateral triangle. A fourth charge Q is placed at the center of the triangle.
A. If Q= - q, will the charges at the corners move toward the center or fly away from it
B. For what value of Q at 0 will the charges remain stationary?

Answer 1

Hint: Since this is an equilateral triangle the angles as well as the length of the sides will be equal. When we place a charge Q at the center of the triangle, the impact on all the other charges kept at the vertex, since equidistant, will be the same. The net resultant force acting on all the vertices of A, B, C of the equilateral triangle will be the sum of the forces due to the charge on other two vertices and the charge at the center.

Formula used:
$F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}$(Coulomb’s Law), $F$is the electrical force between two charged objects, ${q_1}$ represents the quantity of charge on object 1 (in Coulombs),${q_2}$ represents the quantity of charge on object 2 (in Coulombs), and $r$ represents the distance of separation between the two objects (in meters) and ${\varepsilon _0}$ is the vacuum permittivity, permittivity of free space.

Complete step by step answer:
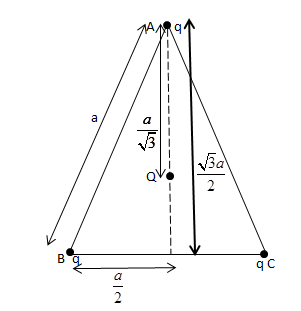
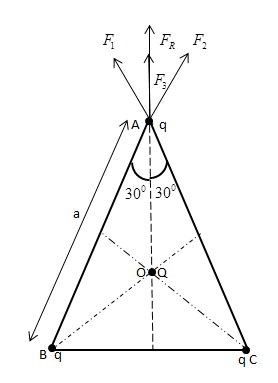
Three charges of equal magnitude are placed at the vertices of an equilateral triangle with side length $a$. First we can find the force along the direction of $O\vec A$. Let the force due to charge q on vertex B be ${F_1}$ and due to charge q on vertex C be ${F_2}$. Using $F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}$(Coulomb’s Law), where $F$ is the electrical force between two charged objects, ${q_1}$ represents the quantity of charge on object 1 (in Coulombs), ${q_2}$ represents the quantity of charge on object 2 (in Coulombs), and $r$ represents the distance of separation between the two objects (in meters) and ${\varepsilon _0}$ is the vacuum permittivity, permittivity of free space. We get,
${F_1} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q^2}\cos ({{30}^0})}}{{{a^2}}}$ along $O\vec A$
${F_2} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q^2}\cos ({{30}^0})}}{{{a^2}}}$ along $O\vec A$
When we place a charge Q at the center O, the force experienced along $O\vec A$ is
${F_3} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{{{{\left( {\dfrac{a}{{\sqrt 3 }}} \right)}^2}}}$
The resultant force ${F_R}$ will be ${F_1} + {F_2} + {F_3}$ since all the forces are taken along the $O\vec A$ direction.
${F_R} = {F_1} + {F_2} + {F_3}$
${F_R} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q^2}\cos ({{30}^0})}}{{{a^2}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q^2}\cos ({{30}^0})}}{{{a^2}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{{{{\left( {\dfrac{a}{{\sqrt 3 }}} \right)}^2}}}$
${F_R} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{a^2}}}\left[ {\sqrt 3 q + 3Q} \right]$

A) Using Q = - q in equation${F_R} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{a^2}}}\left[ {\sqrt 3 q + 3Q} \right]$, we get
${F_R} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{a^2}}}\left[ {\sqrt 3 q - 3q} \right]$along $O\vec A$
${F_R} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{\sqrt 3 {q^2}}}{{{a^2}}}\left[ {1 - \sqrt 3 } \right]$along $O\vec A$
${F_R} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{\sqrt 3 {q^2}}}{{{a^2}}}\left[ {\sqrt 3 - 1} \right]$along $A\vec O$
B) Charge will remain stationary if ${F_R}$ = 0
For ${F_R} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{a^2}}}\left[ {\sqrt 3 q + 3Q} \right]$=0
$\left[ {\sqrt 3 q + 3Q} \right] = 0$
$Q = \dfrac{{ - q}}{{\sqrt 3 }}$
If $Q = \dfrac{{ - q}}{{\sqrt 3 }}$, the charges will remain stationary.

Note: Using Pythagoras theorem the length of the altitude of the triangle can be found to be $\dfrac{{\sqrt 3 a}}{2}$. Remember that the angle bisector of an equilateral triangle will bisect the opposite side. For an equilateral triangle the center O divides the altitude (since the triangle is equilateral, the length of perpendicular from any vertex will be the same.) in the ratio ${2:1}$Therefore the length OA will be two by third of the total length.
$OA = \dfrac{2}{3} \times \dfrac{{\sqrt 3 a}}{2} = \dfrac{a}{{\sqrt 3 }}$