Question
Question: Three charges each of q are arranged at three corners of an equilateral triangle of side a. The elec...
Three charges each of q are arranged at three corners of an equilateral triangle of side a. The electric field at the mid point of one side
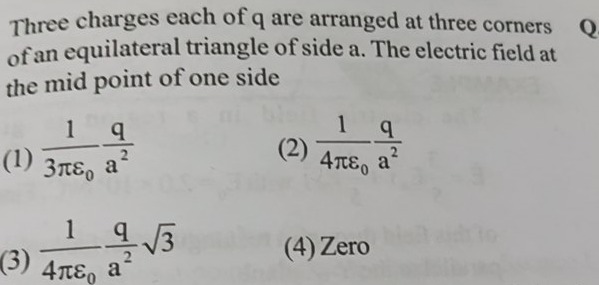
3πϵ01a2q
4πϵ01a2q
4πϵ01a2q3
Zero
3πϵ01a2q
Solution
Let the equilateral triangle be ABC with side length 'a'. Let charges +q be placed at each vertex A, B, and C. We want to find the electric field at M, the midpoint of side BC.
-
Electric field at M due to charge at B:
The distance BM is a/2. The electric field EB at M due to the charge at B is directed along the line segment BM, away from B. The magnitude is EB=4πϵ01(a/2)2q=4πϵ01a24q. The direction is along BC, pointing from B to C. -
Electric field at M due to charge at C:
The distance CM is a/2. The electric field EC at M due to the charge at C is directed along the line segment CM, away from C. The magnitude is EC=4πϵ01(a/2)2q=4πϵ01a24q. The direction is along CB, pointing from C to B. -
Vector sum of electric fields due to B and C:
The vectors EB and EC have the same magnitude (EB=EC) but are in opposite directions along the line BC. Therefore, their vector sum is zero: EB+EC=0. -
Electric field at M due to charge at A:
The distance AM is the altitude of the equilateral triangle from vertex A to the midpoint M of the opposite side BC. The length of the altitude is h=23a.
The electric field EA at M due to the charge at A is directed along the line segment AM, away from A. The magnitude is EA=4πϵ01(AM)2q=4πϵ01(23a)2q=4πϵ0143a2q=4πϵ013a24q. The direction is along AM, pointing from A towards M, which is perpendicular to BC. -
Total electric field at M:
The total electric field at M is the vector sum of the fields due to the three charges: EM=EA+EB+EC.
Since EB+EC=0, the total electric field is EM=EA.
The magnitude of the total electric field at M is EM=EA=4πϵ013a24q.
Comparing this magnitude with the given options: 4πϵ013a24q=34⋅4πϵ01a2q=3πϵ01a2q.
