Solveeit Logo
Login

Question

Question: Three charges each have \( +q \) charge, are placed at the corner of an isosceles triangle ABC of si...

Three charges each have +q+q charge, are placed at the corner of an isosceles triangle ABC of sides BC and AC, 2a.D and E are the mid points of BC and CA. The work done in taking a charge Q from D to E is:

(A) eqQ8π∈0a\dfrac{eqQ}{8\pi {{\in }_{0}}a}
(B) qQ4π∈0a\dfrac{qQ}{4\pi {{\in }_{0}}a}
(C) Zero
(D) 3qQ4π∈0a\dfrac{3qQ}{4\pi {{\in }_{0}}a}

Explanation

Solution

To find out the work done is taking charge Q from one point to another, we will find electrostatic potential at those points using
V=q4π∈0rV=\dfrac{q}{4\pi {{\in }_{0}}r}
VV is the potential generated between the charges
qq is the charge due to which our test charge is affected
r is the distance between the charges.

Complete step by step solution

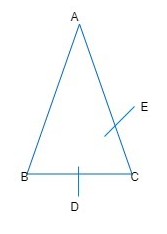
Here,
AC=BC=2aAC=BC=2a
As D and E are midpoints of BC and AC (given).
∴\therefore AE=EC=aAE=EC=a
And,
BD=DC=aBD=DC=a
In ΔADC,\Delta ADC,
(AD)2=(AC)2−(DC)2 =(2a)2−(a)2=(4a)2−(a)2=(a)2 AD=a3 \begin{aligned} & {{(AD)}^{2}}={{(AC)}^{2}}-{{(DC)}^{2}} \\\ & ={{(2a)}^{2}}-{{(a)}^{2}}={{(4a)}^{2}}-{{(a)}^{2}}={{(a)}^{2}} \\\ & AD=a\sqrt{3} \\\ \end{aligned}
Similarly, potential at points D due to the given charge distribution is
VD=14π∈0[qBD+qDC+qAD]{{V}_{D}}=\dfrac{1}{4\pi {{\in }_{0}}}[\dfrac{q}{BD}+\dfrac{q}{DC}+\dfrac{q}{AD}]
=q4π∈0[1a+1a+13a] =q4π∈0a[2+13] \begin{aligned} & =\dfrac{q}{4\pi {{\in }_{0}}}\left[ \dfrac{1}{a}+\dfrac{1}{a}+\dfrac{1}{\sqrt{3}a} \right] \\\ & =\dfrac{q}{4\pi {{\in }_{0}}a}\left[ 2+\dfrac{1}{\sqrt{3}} \right] \\\ \end{aligned} ...........................(1)
Potential at point E due to given charge configuration is
VE=14π∈0[1q+1q+1a3]{{V}_{E}}=\dfrac{1}{4\pi {{\in }_{0}}}\left[ \dfrac{1}{q}+\dfrac{1}{q}+\dfrac{1}{a\sqrt{3}} \right]
=q4π∈0a[2+13]=\dfrac{q}{4\pi {{\in }_{0}}a}\left[ 2+\dfrac{1}{\sqrt{3}} \right] ...........................(2)
From (1) and (2), it is clear that
The work done in taking a charge Q from D to E is
W=Q(VE−VD)=0W=Q({{V}_{E}}-{{V}_{D}})=0 (∵VD=VE)(\because {{V}_{D}}={{V}_{E}})
Therefore, option (C) is correct.

Note
Electric potential due to single charge is spherically symmetric. It should be clearly borne in mind that due to single charge,
F∝1r2F\propto \dfrac{1}{{{r}^{2}}} ; E∝1r2E\propto \dfrac{1}{{{r}^{2}}} but V∝1rV\propto \dfrac{1}{r} ,
where r is the distance from the charge.