Question

Three charges $1\mu C$, $1\mu C$ and $2\mu C$ are kept at the vertices A, B and C respectively of an equilateral triangle ABC of $10cm$ side. The resultant force on the charge at the vertex C is:
A) $0.9 N$
B) $1.8 N$
C) $2.72 N$
D) $3.12 N$

Answer 1

The given charges are kept at the vertices A, B and c respectively of an equilateral triangle ABC of $10cm$. Also we have to find the resultant force on the charge at the vertex C.
Consider a closed ABC triangle, and C will take a force on the charge. The diagram shown below.

Complete step by step answer:
The diagram will be like this,

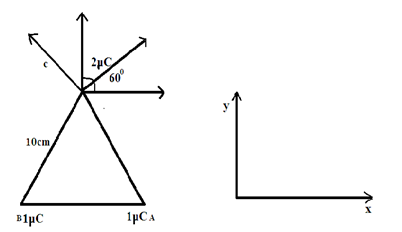
An equiangular triangle has three equal sides and angles. It will always have an angle of ${60^ \circ }$ in each corner.
Component of force due to B and A in x direction acting on C cancel out each other
$\therefore {F_x} = 0$
In $y$ direction forces add up
We get ${F_x} = \dfrac{{k(1\mu C)(2\mu C)}}{{{{(10 \times {{10}^{ - 2}})}^2}}} \times \sin 60 \times 2$
Substitute the values, and $\sin 60 = \dfrac{{\sqrt 3 }}{2}$
$\Rightarrow \dfrac{{9 \times {{10}^9} \times 1 \times {{10}^{ - 6}} \times 2 \times {{10}^{ - 6}}}}{{100 \times {{10}^{ - 6}}}} \times \dfrac{{\sqrt 3 }}{2} \times 2$
Cancelling the same term and multiply to the remaining terms, we get
So we get,
$\Rightarrow 3.1176N$

So, The correct answer is option (D).

Additional information:
In geometry, a triangle may be a closed, two-dimensional shape with three straight sides. A triangle is also a polygon. A triangle with all sides equilateral, a triangle with two sides equal is called isosceles, and a triangle with all sides a different length is called scalene.

Note: Triangles are often broadly classified into two types, which are:
Triangle based on the lengths of their sides
A) According to the lengths of their sides, triangles can be classified into three types with are:
i) Scalene
ii) Isosceles
iii) Equilateral

Triangles based on the their interior angles
B) According to the their interior angles, triangles can be classified into three types with are:
i) Acute-angled
ii) Obtuse-angled
iii) Right-angled