Question

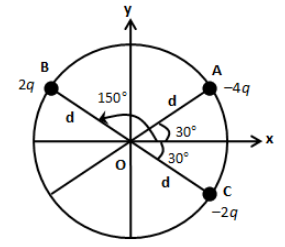
Three charged particles A, B and C with charges $- 4q$, $2q$ and $- 2q$ are present on the circumference of a circle of radius d. The charged particles A, C and centre O of the circle formed an equilateral triangle as shown in the figure. Electric field at O along x-direction is:

Answer 1

The imaginary test charge at point O, will be attracted by charges A and C and repelled by charge B. So, the direction of the electric field at point O due to charges $- 4q$and $- 2q$ is towards A and C respectively. Also, the electric field at point o due to charge $2q$ is towards point C. Calculate the x-component of the electric field at point O by taking the addition of electric fields due to each charge.

Formula used:
Electric field, $E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{d^2}}}$,
where, ${\varepsilon _0}$ is the permittivity of free space, q is the charge and d is the distance.

Complete step by step answer:
We know the like charges repel each other while unlike charges attract towards each other. Therefore, the imaginary test charge at point O, will be attracted by charges A and C and repelled by charge B. So, the direction of the electric field at point O due to charges $- 4q$and $- 2q$ is towards A and C respectively. Also, the electric field at point o due to charge $2q$ is towards point C as shown in the figure below.

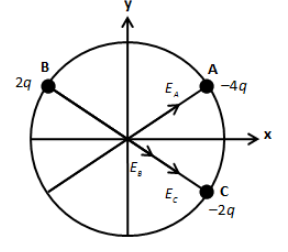
Let us express the magnitude of electric field at point O due to charge $- 4q$ as follows,
${E_A} = k\dfrac{{ - 4q}}{{{d^2}}}$ …… (1)
Here, k is the constant and it has value $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$, where, ${\varepsilon _0}$ is the permittivity of the free space.

Let us express the magnitude of electric field at point O due to charge $2q$ as follows,
${E_B} = k\dfrac{{2q}}{{{d^2}}}$ …… (2)
Let us express the magnitude of electric field at point O due to charge $- 2q$ as follows,
${E_C} = k\dfrac{{ - 2q}}{{{d^2}}}$ …… (3)
The direction of the electric field at point O along the horizontal direction x is can be expressed as,
${E_x} = {E_A}\cos 30^\circ + {E_B}\cos 30^\circ + {E_C}\cos 30^\circ$
$\Rightarrow {E_x} = \left( {{E_A} + {E_B} + {E_C}} \right)\cos 30^\circ$
$\Rightarrow {E_x} = \left( {{E_A} + {E_B} + {E_C}} \right)\dfrac{{\sqrt 3 }}{2}$
Using equation (1), (2) and (3) in the above equation, we get,
${E_x} = \left( {k\dfrac{{ - 4q}}{{{d^2}}} + k\dfrac{{2q}}{{{d^2}}} + k\dfrac{{ - 2q}}{{{d^2}}}} \right)\dfrac{{\sqrt 3 }}{2}$
$\Rightarrow {E_x} = k\dfrac{q}{{{d^2}}}\left( { - 4 + 2 + - 2} \right)\dfrac{{\sqrt 3 }}{2}$
$\therefore {E_x} = - 2\sqrt 3 \,k\dfrac{q}{{{d^2}}}$

This is the expression for the horizontal component of the electric field at point O.

Note: The crucial step in the solution is to determine the direction of the electric field due to the given charges. If the charge at B is negative, then the direction of the electric field would be towards the charge. The x-component of this electric field would be along the negative x-axis. Note that $\cos \left( { - \theta } \right) = \cos \theta$.