Question
Question: Three Carnot engines operate in series between a heat source at a temperature \({{\text{T}}_1}\) and...
Three Carnot engines operate in series between a heat source at a temperature T1 and a heat sink at a temperature T4 (see figure). There are two other reservoirs at temperatures T2 and T3, as shown, with T1>T2>T3>T4. The three engines will be equally efficient if
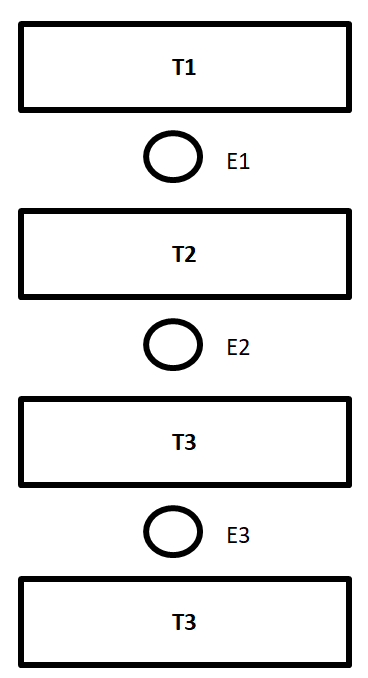
(A) T2=(T12T4)1/3;T3=(T1T42)1/3
(B) T2=(T1T42)1/3;T3=(T12T4)1/3
(C) T2=(T13T4)1/4;T3=(T1T43)1/4
(D) T2=(T1T4)1/2;T3=(T12T4)1/3
Solution
Hint To solve this question, we have to use the expression of the efficiency of a heat engine, for the three engines given. Then, we have to equate the three efficiencies to get three equations, with the help of which we will get the answer.
The formula used to solve this question is
⇒η=1−TsourceTsink, where is the efficiency of a heat engine having Tsource as the temperature of the heat source and Tsink as the temperature of the heat sink.
Complete step by step answer
Let η1, η2 and η3 be the efficiencies of the heat engines ⇒E1,E2 and E3 respectively.
For the heat engine E1
As we know that the heat source has a higher temperature than the heat sink.
∵T1>T2
So, T1 is the temperature of the heat source, and T1 is the temperature of the heat sink.
Now, we know that the efficiency of a heat engine is given by
⇒η=1−TsourceTsink
So, the efficiency of the first heat engine
⇒η1=1−T1T2 (1)
Similarly,
⇒η2=1−T4T3, and (2)
⇒η3=1−T3T4 (3)
According to the question, η1=η2=η3
Equating (1) and (2), we get
⇒1−T1T2=1−T2T3
So that
⇒T1T2=T2T3
By cross multiplying, we get
⇒T22=T1T3 (4)
Equating (2) and (3), we get
⇒1−T2T3=1−T3T4
So that
⇒T2T3=T3T4
By cross multiplying, we get
⇒T32=T2T4 (5)
Equating (1) and (3), we get
⇒1−T1T2=1−T3T4
So that
⇒T1T2=T3T4
⇒T2=T3T1T4 (6)
Dividing (4) by (5)
⇒(T3T2)2=T2T4T1T3
Multiplying by T3T2 both the sides
⇒(T3T2)3=T4T1
⇒T3T2=(T4T1)1/3
⇒T2=(T4T1)1/3T3 (7)
Substituting (6)
⇒T3T1T4=(T4T1)1/3T3
⇒T32=T12/3T44/3
Taking square root
⇒T3=T11/3T42/3
⇒T3=(T1T42)1/3
Substituting in (7)
⇒T2=(T4T1)1/3(T1T42)1/3
⇒T2=T12/3T41/3
Or
⇒T2=(T12T4)1/3
Therefore, T2=(T12T4)1/3and T3=(T1T42)1/3
Hence, the correct answer is option (A).
Note
To solve these types of problems involving multiple variables, we just need to see in the options what variables are to be found out. We just need to separate those variables and write them in the form of remaining variables from the equations formed.
