Question

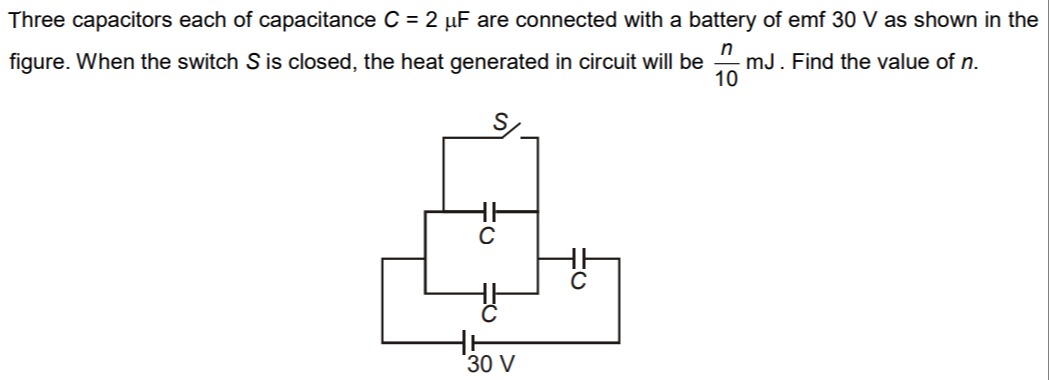
Three capacitors each of capacitance $C = 2 \mu F$ are connected with a battery of emf 30 V as shown in the figure. When the switch S is closed, the heat generated in circuit will be $\frac{n}{10} mJ$. Find the value of $n$.

Answer 1

19.5

Answer 2

The heat generated in the circuit when the switch is closed is given by $H = W_{battery} - \Delta U$, where $W_{battery}$ is the work done by the battery and $\Delta U$ is the change in the total potential energy stored in the capacitors. The work done by the battery is $W_{battery} = V \Delta Q$, where $V$ is the battery voltage and $\Delta Q$ is the total charge supplied by the battery.

Initial state (switch open):

Let the potential of the bottom wire connected to the positive terminal of the battery be $V_+ = 30V$ and the potential of the point connected to the negative terminal be $V_- = 0V$. Let the potential of the middle wire be $V_m$ and the potential of the top wire be $V_t$. The bottom capacitor $C_1$ is connected between $V_+$ and $V_m$. The middle capacitor $C_2$ is connected between $V_m$ and $V_t$. The right capacitor $C_3$ is connected between $V_m$ and $V_-$. With the switch open, the top wire is isolated. Assuming the capacitors were initially uncharged before connecting the battery, and then the battery was connected with the switch open, the net charge on the isolated plates (top plate of $C_2$) remains zero. However, if the circuit has been in this configuration for a long time, the potentials will be determined by the connections.

Let's assume the interpretation of the diagram where the bottom wire is at 30V, the right point is at 0V.

Initial state (switch open): Capacitor $C_1$ is between 30V and $V_m$. Capacitor $C_2$ is between $V_m$ and $V_t$. Capacitor $C_3$ is between $V_m$ and 0V. Since the top wire is isolated, no charge flows to it. If the capacitors were initially uncharged, then the charge on the top plate of $C_2$ is $q_{2,top} = C(V_t - V_m)$. Since the wire is isolated, $q_{2,top}$ should be zero. This implies $V_t = V_m$. If $V_t = V_m$, then the potential difference across $C_2$ is zero, so its initial charge and energy are zero. Then $C_1$ is between 30V and $V_m$, and $C_3$ is between $V_m$ and 0V. These two capacitors are in series connected between 30V and 0V. Equivalent capacitance of $C_1$ and $C_3$ in series is $C_{13} = \frac{C \times C}{C + C} = \frac{C}{2}$. The potential difference across the series combination is 30V. The charge on each capacitor is $Q_{initial} = C_{13} \times 30 = \frac{C}{2} \times 30 = 15C$. $V_m$ is the potential between $C_1$ and $C_3$. Potential difference across $C_3$ is $V_m - 0 = V_m$. Charge on $C_3$ is $C V_m = 15C$. So $V_m = 15V$. Potential difference across $C_1$ is $30 - V_m = 30 - 15 = 15V$. Charge on $C_1$ is $C(30 - V_m) = C(15) = 15C$. This is consistent. So, in the initial state (switch open), $V_m = 15V$ and $V_t = 15V$. Initial potential energy stored in the capacitors: $U_{initial} = \frac{1}{2} C_1 (30 - V_m)^2 + \frac{1}{2} C_2 (V_t - V_m)^2 + \frac{1}{2} C_3 (V_m - 0)^2$ $U_{initial} = \frac{1}{2} C (30 - 15)^2 + \frac{1}{2} C (15 - 15)^2 + \frac{1}{2} C (15 - 0)^2$ $U_{initial} = \frac{1}{2} C (15)^2 + 0 + \frac{1}{2} C (15)^2 = 2 \times \frac{1}{2} C (225) = 225C$.

Final state (switch closed): The switch connects the top wire to the 0V terminal. So $V_t = 0V$. Capacitor $C_1$ is between 30V and $V_m$. Capacitor $C_2$ is between $V_m$ and $V_t = 0V$. Capacitor $C_3$ is between $V_m$ and 0V.

Let's use nodal analysis in the final state. Let $V_m$ be the potential of the middle wire. The bottom wire is at 30V, and the top wire and the right point are at 0V. Charge conservation at node $V_m$: The sum of charges on the plates connected to $V_m$ is zero. The top plate of $C_1$ is at $V_m$, bottom plate at 30V. Charge on top plate is $Q_{1,top} = C(V_m - 30)$. The bottom plate of $C_2$ is at $V_m$, top plate at 0V. Charge on bottom plate is $Q_{2,bottom} = C(V_m - 0) = C V_m$. The top plate of $C_3$ is at $V_m$, bottom plate at 0V. Charge on top plate is $Q_{3,top} = C(V_m - 0) = C V_m$. Sum of charges on the plates connected to $V_m$: $Q_{1,top} + Q_{2,bottom} + Q_{3,top} = 0$. $C(V_m - 30) + C V_m + C V_m = 0$ $V_m - 30 + V_m + V_m = 0$ $3V_m = 30$ $V_m = 10V$.

Final potential energy stored in the capacitors: $U_{final} = \frac{1}{2} C_1 (30 - V_m)^2 + \frac{1}{2} C_2 (V_m - V_t)^2 + \frac{1}{2} C_3 (V_m - 0)^2$ $U_{final} = \frac{1}{2} C (30 - 10)^2 + \frac{1}{2} C (10 - 0)^2 + \frac{1}{2} C (10 - 0)^2$ $U_{final} = \frac{1}{2} C (20)^2 + \frac{1}{2} C (10)^2 + \frac{1}{2} C (10)^2 = \frac{1}{2} C (400) + \frac{1}{2} C (100) + \frac{1}{2} C (100)$ $U_{final} = 200C + 50C + 50C = 300C$.

Change in potential energy: $\Delta U = U_{final} - U_{initial} = 300C - 225C = 75C$.

Work done by the battery: $W_{battery} = V \Delta Q$, where $\Delta Q$ is the total charge supplied by the battery from the positive terminal. The positive terminal is connected to the bottom wire.

The change in charge on the bottom plate of $C_1$ is $20C - (-15C) = 35C$. This is the charge that flowed from the battery. So, $\Delta Q = 35C$. Work done by the battery: $W_{battery} = 30V \times 35C = 1050C$.

Heat generated: $H = W_{battery} - \Delta U = 1050C - 75C = 975C$. Given $C = 2 \mu F = 2 \times 10^{-6} F$. $H = 975 \times 2 \times 10^{-6} J = 1950 \times 10^{-6} J = 1.95 \times 10^{-3} J = 1.95 mJ$.

The heat generated is given as $\frac{n}{10} mJ$. So, $1.95 mJ = \frac{n}{10} mJ$. $1.95 = \frac{n}{10}$ $n = 1.95 \times 10 = 19.5$.