Question

Three capacitors each of $6 \mu F$ are connected in series and then connected in series with the parallel combination of three capacitors of $2\mu F$, $4\mu F$ and $2\mu F$. The total combined capacity is:
$A. 2\mu F$
$B. 10\mu F$
$C. 12\mu F$
$D. 1.6 \mu F$

Answer 1

To solve this problem, first find the equivalent capacitance of the three capacitors each of $6 \mu F$ which are connected in series. Then, find the equivalent capacitance of the three capacitors of $2\mu F$, $4\mu F$ and $2\mu F$ which are connected in parallel. It is given that the three capacitors in series are connected in series with the parallel combination. So, find the equivalent combination of the equivalent capacitance of series combination and parallel combination.

Complete answer:

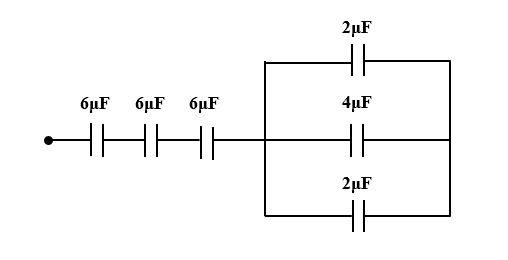
Let the three capacitors in series be ${C}_{1}$, ${C}_{2}$ and ${C}_{3}$ respectively. The three capacitors in parallel are ${C}_{4}$, ${C}_{5}$ and ${C}_{6}$ respectively.
Given: ${C}_{1}= {C}_{2}={C}_{3}= 6 \mu F$
${C}_{4}= 2\mu F$
${C}_{5}= 4\mu F$
${C}_{6}= 2\mu F$
Capacitors ${C}_{1}$, ${C}_{2}$ and ${C}_{3}$ are connected in series. So, their equivalent capacitance will be given by,
$\dfrac { 1 }{ { C }_{ { eq }_{ 1 } } } =\dfrac { 1 }{ { C }_{ 1 } } +\dfrac { 1 }{ { C }_{ 2 } } +\dfrac { 1 }{ { C }_{ 3 } }$
Substituting values in above equation we get,
$\Rightarrow \dfrac { 1 }{ { C }_{ { eq }_{ 1 } } } =\dfrac { 1 }{ 6 } +\dfrac { 1 }{ 6 } +\dfrac { 1 }{ 6 }$
$\Rightarrow \dfrac { 1 }{ { C }_{ { eq }_{ 1 } } } =\dfrac { 3 }{ 6 }$
$\Rightarrow \dfrac { 1 }{ { C }_{ { eq }_{ 1 } } } =\dfrac { 1 }{ 2 }$
$\Rightarrow { C }_{ { eq }_{ 1 } }=2\mu F$
Capacitors ${C}_{4}$, ${C}_{5}$ and ${C}_{6}$ are connected in parallel. So, their equivalent capacitance will be given by,
${ C }_{ { eq }_{ 2 } }={ C }_{ 4 }+{ C }_{ 5 }+{ C }_{ 6 }$
Substituting values in above equation we get,
${ C }_{ { eq }_{ 2 } }=2+4+2$
$\Rightarrow { C }_{ { eq }_{ 2 } }=8 \mu F$
Combination of capacitors in series is connected in series with the combination of capacitors in parallel. So, their equivalent capacitance will be given by,
$\dfrac { 1 }{ { C }_{ T } } =\dfrac { 1 }{ { C }_{ { eq }_{ 1 } } } +\dfrac { 1 }{ { C }_{ { eq }_{ 2 } } }$
Substituting values in above equation we get,
$\dfrac { 1 }{ { C }_{ T } } =\dfrac { 1 }{ 2 } +\dfrac { 1 }{ 8 }$
$\Rightarrow \dfrac { 1 }{ { C }_{ T } } =\dfrac { 10 }{ 16 }$
$\Rightarrow \dfrac { 1 }{ { C }_{ T } } =\dfrac { 5 }{ 8 }$
$\Rightarrow {C}_{T}= \dfrac {8}{5}$
$\Rightarrow {C}_{T}= 1.6\mu F$
Thus, the total combined capacity is $1.6 \mu F$.

So, the correct answer is option D i.e. $1.6\mu F$.

Note:
Students must remember that when the capacitors are connected in series, the total capacitance is less than at least any one of the series capacitors individual capacitance. When capacitors are connected in parallel, the total capacitance is the sum of all the capacitors’ capacitances. Students should remember that the formula for total capacitance is not the same as that for total resistance. So, students should not get confused between the formula for capacitance and resistance in series and capacitance and resistance in parallel.