Question

Three boys and three girls are to be seated around a table in a circle. Among them, the boy X does not want any girl neighbor and the girl Y does not want any boy neighbor. How many such arrangements are possible?
(a) 5
(b) 6
(c) 4
(d) 2

Answer 1

Hint- In this question, we will fix the position of boy X in between two boys as mentioned in the question and similarly fix the position of girl Y in between two girls and then calculate the number of ways in which other boys and girls will arrange themselves.
As given in the question, there are three boys and three girls who wanted to sit together in a circle but with some conditions.

Complete step-by-step solution -
Let 3 boys are $B_1, B_2$ and X
And similarly 3 girls are $G_1, G_2$ and Y

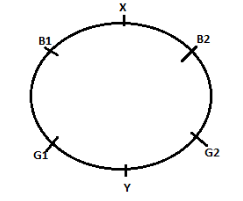
According to the first condition, the boy X does not want any girl neighbor. It means that the boy X does not want to sit adjacent to any girl. So, there is only one way in which boy X can sit which is between two other boys that is $B_1$ and $B_2$. That is, the neighbor of boy X will be the other two boys.
So, the number of ways in which $B_1$ and $B_2$ boys can arrange themselves will be equal to
$= 2! \\\ = 2 \\\$
Similarly, the girl Y does not want to sit adjacent to any boy. So, there is only one way in which girl Y can seat which is between two other girls. That is, the neighbor of girl Y will be the other two girls.
So, the number of ways in which the girls $G_1$ and $G_2$ can arrange themselves will be equal to
$= 2! \\\ = 2 \\\$
$\therefore$ The total number of ways in which all girls and boys will seat together in circle with above mentioned conditions is
$= 2!*2! \\\ = 4 \\\$

Note- For solving these types of questions, we should know the basic permutation concepts. Like in the above question, there are two persons which can sit in two different positions, so the number of ways in which two persons can sit on those seats is $2{P_2}$ which can be solved as 2!