Question

Three blocks of masses${m_1}$, ${m_2}$ and ${m_3}$ are connected by massless strings as shown on a frictionless table. They are pulled with a force of $40N$. If ${m_1} = 10kg$, ${m_2} = 6kg$and ${m_3} = 4kg$, then tension ${T_2}$will be:-

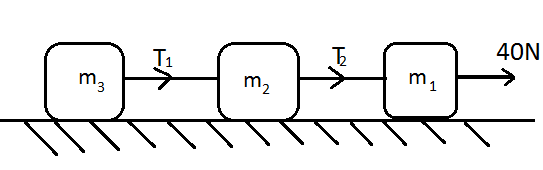
(A) $10N$
(B) $20N$
(C) $32N$
(D) $40N$

Answer 1

The whole system of blocks is moving with an acceleration which is equal to the product of the force applied on the system and the sum of all the masses. Once we calculate the acceleration of the system, the tension can be calculated.

Complete step by step answer:
The system of blocks will move with an acceleration when a force of $40N$is applied on it. This acceleration can be calculated by the formula,
$F = ma$
$a = \dfrac{F}{m}$
$F = 40N$ (given)
$a$is acceleration of the whole system
$m$is the sum of all the masses.
Putting the values in the above formula, we get,
$a = \dfrac{{40}}{{\left( {10 + 6 + 4} \right)}} = 2m/{s^2}$

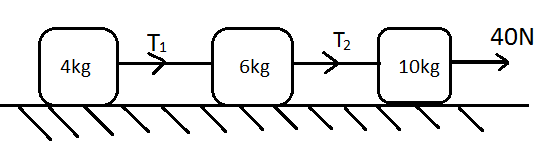
If we consider each block separately, we see that the force ${T_1}$ is required to pull the$4kg$ block so we can write the equation for this block as,
${T_1} = {m_3}a = 4 \times 2 = 8N$
For the second block, we see that the force ${T_2}$is required to pull $4kg$and $6kg$block, so for this we can write the equation as,

$${T_2} = {m_3}a + {m_2}a \\\ {T_2} = 8 + \left( {6 \times 2} \right) = 20N \\\$$

Thus, the tension ${T_2} = 20N$. Hence, the correct option is B.

Additional Information: If the positions of the blocks are changed, the acceleration of the system remains the same but the tension in each string changes. While calculating, we must consider the position and mass of the block to find out the correct tension in each string. Besides this, the consideration of the type of force (push or pull) and the angle at which the force is applied is also important.

Note: For the second block we can make another equation also. The force required to accelerate the particular $6kg$block will be ${T_2} - {T_1}$ and this force will be equal to the mass of second block and its acceleration which is given by the following equation,

$${T_2} - {T_1} = {m_2}a \\\ {T_2} = {m_2}a + {T_1} \\\ {T_2} = 12 + 8 = 20N \\\$$

By considering each block separately, it becomes easier to calculate the tension in each string.