Question

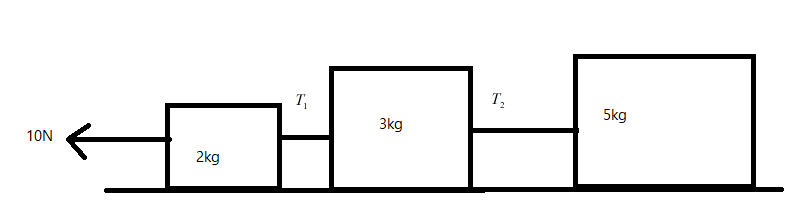
Three blocks of masses $2\; kg,3\; kg$ and $5\; kg$ are connected to each other with a light wire and placed on a frictionless surface. The system is pulled by a force $F=10N$ then the tension on $T_{1}$ is:

& A.1N \\\ & B.8N \\\ & C.5N \\\ & D.10N \\\ \end{aligned}$$

Answer 1

Consider the given diagram in the question as a system. Then are two forces that act on the system. One is the tension on the string, and the other is the force exerted. Then the two forces must be equal for the whole system to be at rest.

Formula used:
$T_{1}+T_{2}=F$ and $F=ma$
Complete step by step answer:
Let us consider the block and strings as a system. Let $F=10N$ be the external force on the system. Let $T_{1}$ be the tension on the string due to block of mass $3\; kg$ and $5\;kg$, and let $T_{2}$ be the tension on the string due to block of mass $5\; kg$ . Let us also assume that the system is at rest.
We know that an external force causes acceleration. Then here the $F=10N$ causes an acceleration $a$. Let us assume that there is no friction, then the $F=ma$. Since the blocks are connected, then the $m$ here is the summation of mass all the given blocks
Then we can say, $10N=(2+3+5)a$
$\implies a=1m/s^{2}$
Since the force $F$ is in the opposite direction of $T$ then, we can say that both are equal for the mass to remain in rest.
Then $F=T_{1}+T_{2}$
Since we need to find the value of $T_{1}$, let us consider the following,

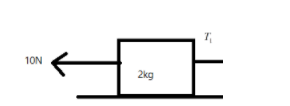
Then, we can say that $F-2a=T_{1}$.
$\implies 10-2=T_{1}$
$\implies T_{1}=8N$
Hence the answer is $B.8N$

Note:
The direction of $T$ and $F$ are $\hat x$ and $-\hat x$ respectively. Then from Newton’s third law, we can say that both are equal. Since, $F=T_{1}+T_{2}$, one can also find the value of $T_{1}$ by finding the $T_{2}$ and then subtract the value from the $F$. Either way is acceptable and will lead to the same answer always.