Question

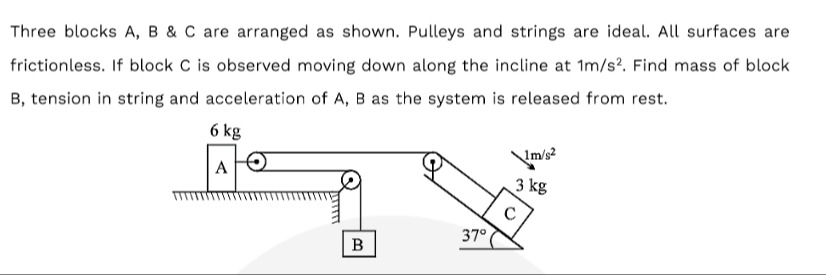
Three blocks A, B & C are arranged as shown. Pulleys and strings are ideal. All surfaces are frictionless. If block C is observed moving down along the incline at 1m/s². Find mass of block B, tension in string and acceleration of A, B as the system is released from rest.

Answer 1

• Mass of block B: ≈ 1.71 kg
• Tension in the string: 3 N (in the string connecting A and B)
• Acceleration of blocks A and B: 0.5 m/s²

Answer 2

We will show that with a proper free‐body diagram and a careful use of the inextensibility conditions the answer comes out uniquely.

In what follows the key is to notice that the block B is connected to two segments of the same string so that it works as a movable “crown” (or pulley) for the string going toward block C. In this arrangement the displacement of block C will be twice that of block B; hence, the (ideal) string constraint gives

a₍C₎ = 2·a₍B₎     (1)

Since we are told that block C is observed to accelerate down the plane at

a₍C₎ = 1 m/s²

it follows that

a₍B₎ = ½ = 0.5 m/s²     (2)

Also, block A is connected by an inextensible string (via a pulley on A) to block B. Hence the acceleration of A (on the frictionless horizontal surface) is

a₍A₎ = a₍B₎ = 0.5 m/s²     (3)

Let us now look at the forces acting.

mermaid flowchart TD A[Block A (6 kg)] -- T₁ --> FP[Fixed Pulley] FP -- "Vertical string" --> B[Block B (m_B)] FP -- "String over 3rd pulley" --> C[Block C (3 kg) on 37° incline]

There are two different strings involved; the one connecting A and B has tension T₁ and the one going from the fixed pulley (via the third pulley) to block C has tension T₂. However, the free‐body diagram on B shows that B “feels” both tensions.

1. For block A (mass = 6 kg) moving horizontally, T₁ = 6·a₍A₎ = 6 × 0.5 = 3 N     (4)

2. For block C (mass = 3 kg) on an incline at 37°: Take the coordinate along the plane (downwards positive). The weight component along the plane is 3g sin 37°. Since the string (with tension T₂) is assumed to be directed up along the plane, 3g·sin 37° – T₂ = 3·(1) Using sin 37° = 0.6 and g = 9.8 m/s², T₂ = 3·9.8×0.6 – 3 = 17.64 – 3 = 14.64 N  (5)

3. For block B (mass = m_B) note that:

   • The upward forces are T₁ (from the string going to A) and T₂ (from the string going toward C via the pulley)
   • The downward force is its weight m_B g. Since we found a₍B₎ = 0.5 m/s² upward, Newton’s 2nd law gives T₁ + T₂ – m_B g = m_B (0.5)    (6)

Now substitute T₁ = 3 N and T₂ = 14.64 N: 3 + 14.64 = m_B(g + 0.5) 17.64 = m_B(9.8 + 0.5) = m_B·10.3 Thus, m_B = 17.64/10.3 ≈ 1.71 kg    (7)

So, our final answers are:

• Mass of block B: m_B ≈ 1.71 kg
• Tension in the string joining A and B: T₁ = 3 N
• Acceleration of blocks A and B: 0.5 m/s²

Short Explanation

1. Constraint: Because block B is the pulley for the string to C, a_C = 2a_B. Given a_C = 1 m/s², we get a_B = 0.5 m/s² (and a_A = 0.5 m/s²).
2. Block A: T₁ = 6×0.5 = 3 N.
3. Block C: Along the incline, 3g sin37° – T₂ = 3×1, so T₂ = 14.64 N.
4. Block B: T₁ + T₂ – m_B g = m_B×0.5; solving gives m_B ≈ 1.71 kg.