Question

Three blocks A, B and C are suspended as shown in the figure. Mass of the blocks A and C is m. If the system is in equilibrium and mass of B is M, then

A. M = 2m
B. M < 2m
C. M > 2m
D. M = m

Answer 1

Mark the tensions in each string. Then draw the free body diagrams for each of the blocks. Equate the tension force and the gravitational force acting on each block because the net force is zero. They find a relation between the three tensions.
Formula used:
F = mg

Complete answer:
It is given that three blocks A, B and C are suspended as shown in the figure. It is said that the system is at rest. If the system is at rest, then the net force on the system must be zero.
In this case, if the net force is zero, then the net forces on all the three blocks will be zero.
Let analyse the forces on all the blocks. For this, we will draw free body diagrams for each of the blocks.
Before let us mark the tensions in the strings. Let the tensions in the strings to which the blocks A, B, C are attached be ${{T}_{1}},{{T}_{2}},{{T}_{3}}$ respectively.
The gravitational force always acts downwards on a body of mass m with a magnitude of mg, where g is acceleration due to gravity.
Therefore, the gravitational forces on the blocks A, B and C are mg, Mg and mg.
Therefore, the free body diagram of block A will be as shown below.

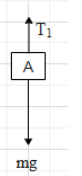
Since the block is at rest, ${{T}_{1}}=mg$ …… (i).
Similarly, the free body diagrams of block B and C will be:

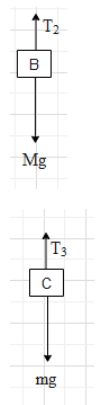
And we get that ${{T}_{2}}=Mg$ ….. (ii) and ${{T}_{3}}=mg$….. (iii).
Now let find the relation between ${{T}_{1}},{{T}_{2}},{{T}_{3}}$.

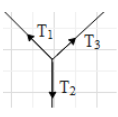
The sum of the vertical components of ${{T}_{1}}$ and ${{T}_{3}}$ will be equal to ${{T}_{2}}$.
But the vertical component of each tension will be less than the actual tension. Hence, the sum of the vertical components of the two tension will be then ${{T}_{1}}+{{T}_{3}}$.
$\Rightarrow {{T}_{1}}+{{T}_{3}}$ > ${{T}_{2}}$.
Substitute the values of ${{T}_{1}},{{T}_{2}},{{T}_{3}}$ from (i), (ii) and (iii).
Then,
$\Rightarrow$mg + mg > Mg.
$\Rightarrow$2m > M.

Hence, the correct option is B.

Note:
We found that the system will be at rest when M < 2m. This means that the mass of block B must be greater than two times the mass of block A.
If M > 2m, then the gravitational force on block B will be greater than the tension force and thus the block will accelerate downwards. As a result, the other two will be accelerated upwards.