Question
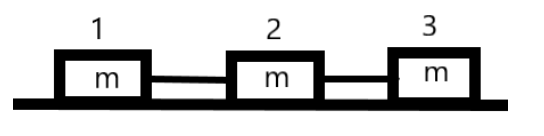
Question: Three blocks 1,2, and 3 rest on a horizontal frictionless surface, as shown. Each block has a mass ‘...
Three blocks 1,2, and 3 rest on a horizontal frictionless surface, as shown. Each block has a mass ‘m’ and the blocks are connected by massless strings. Block 3 is pulled to the right by a force F. The resultant force on block 2 is:
Solution
The resultant force acting on the block 2 due to the force acting on the block 3 can be computed easily using the appropriate relations. The floor is given to be frictionless so we have to consider just the forces due to the external force F and the masses.
Complete step by step answer:
We are given three equal masses connected by massless strings as shown in the figure. They are pulled to the right by a force F acting on the mass 3. The other two masses are pulled by the resultant force acting on each of the blocks.
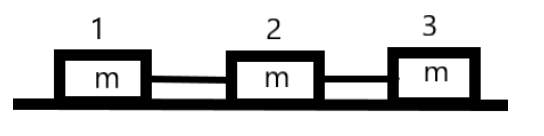
Now, let us consider the force acting on the block 3 which pulls the three blocks with equal acceleration and therefore, equal force as the masses are equal. The net force acting on the system is given by F. We can derive the acceleration on the system using the Newton’s second law of motion –
F=Ma
Where M is the total mass of the system which is equal to 3m,
a is the acceleration of the system.
The acceleration is given by –
