Question
Question: Three balls \(A,B\) and \(C\) \(\left( {{m_A} = {m_C} = 4{m_B}} \right)\) are placed on a smooth hor...
Three balls A,B and C (mA=mC=4mB) are placed on a smooth horizontal surface. The ball B collides with a ball C with an initial velocity v as shown. The total number of collisions between the balls will be (all collisions are elastic)
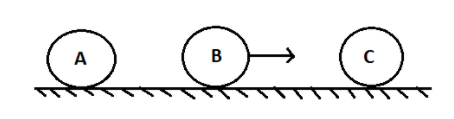
(A) One
(B) Two
(C) Three
(D) Four
Solution
Hint Given that three balls are placed on a smooth surface. Ball A and ball C are of equal mass. They have mass 4 times that of the ball B. It says that the ball B will collide with C. We have to find out the number of collisions between the balls. It is given that the collisions are elastic.
Complete Step by step solution
The velocity of the ball B before the collision is given as v
After the collision,
Assume that the velocity of C=v1
And the velocity of B=v2
Hence we can write,
v=v1+v2
v2 will be in the opposite direction of v1.
From the equation, v=v1+v2
We can write,
v1=v−v2
We know that the momentum can be written as, P=mv
Here applying the conservation of momentum,
mBv=mBv2+mCv1
Since mC=4mB
Substituting mC=4mBin the above equation we get
mBv=mBv2+4mBv1
Eliminating the common terms
We get,
v=v2+4v1………………………………………………(1)
For an elastic collision, the coefficient of restitution is defined as the ratio of the velocity of separation and to the velocity of approach, i.e.
e=vAvS
Where e stands for the coefficient of restitution, vS stands for the velocity of separation, and vAstands for the velocity of approach.
Here, we know that the velocity of separation will be, vA=−(v2−v1)=v1−v2
The velocity of approach will be, vA=v
Hence e can be written as,
e=vv1−v2
For elastic collision e=1
Hence we can write,
vv1−v2=1
⇒v1−v2=v…………………………………………………………………….(2)
Adding equation (1) and equation (2) we get,
v2+4v1=v+
v1−v2=v
⇒5v1=2v
Solving the above equation,
v1=52v
Substituting the value of v1 in equation (2) we get,
52v−v2=v
⇒52v−v=v2
From this we get,
v2=−53v
Now the ball C will move with a velocity 52v and the ball B will move with a velocity 53v in opposite directions.
The ball B will hit the ball A with a velocity −53v
Let v3be the velocity of the ball A
Applying the law of conservation of momentum again, we get
mB(−53v)=−mAv3+mBvˉ2
We know that mA=4mB
Substituting, we get
mB(−53v)=−4mBv3+mBv2
Canceling common terms,
−53v=−4v3+vˉ2………………………………………………………………………………..(3)
Again considering the coefficient of restitution,
e=vAvS
Where e stands for the coefficient of restitution, vS stands for the velocity of separation, and vA stands for the velocity of approach.
Here, we know that the velocity of separation will be, vA=−(−v3−vˉ2)=v3+vˉ2
The velocity of approach will be, vA=53v
e=53vv3+vˉ2
Here also the collision is elastic, hence e=1
53v=v3+vˉ2……………………………………………………………………………..(4)
Multiplying 4with equation (4) and adding with equation (3), we get
512v=4v3+4vˉ2+
5−3v=−4v3+vˉ2
This will give us,
59v=5vˉ2
From this, we get
vˉ2=259v
Substituting in equation (4)
53v=v3+259v
From this,
v3=53v−259v
⇒v3=256v
Now the ball A will be moving with a velocity 256v and the ball B will be moving with a velocity 259v in the opposite direction. The state will be as shown below
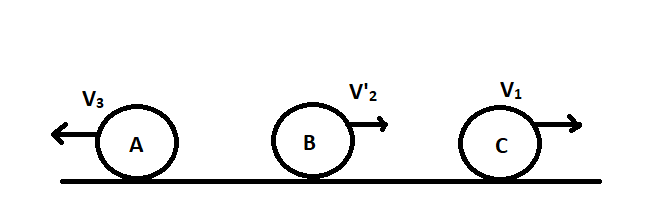
We know that vˉ2=259vand v1=52v
⇒vˉ2≪v1
Hence there will not be the third collision. Therefore there will only be two collisions.
The answer is Option (B): Two
Note
In all collisions, the total linear momentum will always be conserved. But the kinetic energy of the system is not always conserved. If the total kinetic energy of a system is conserved after collision such collisions are called elastic collisions and if the total kinetic energy of a system is not conserved after collision then the collision is called an inelastic collision.
