Question

A conducting wire bent in the form of a parabola $y^2 = x$, is carrying a current /= 1 A in anticlockwise sense as shown. This wire is placed in a uniform magnetic field $\overrightarrow{B} = -2\hat{k}$ tesla. The unit vector in the direction of force is

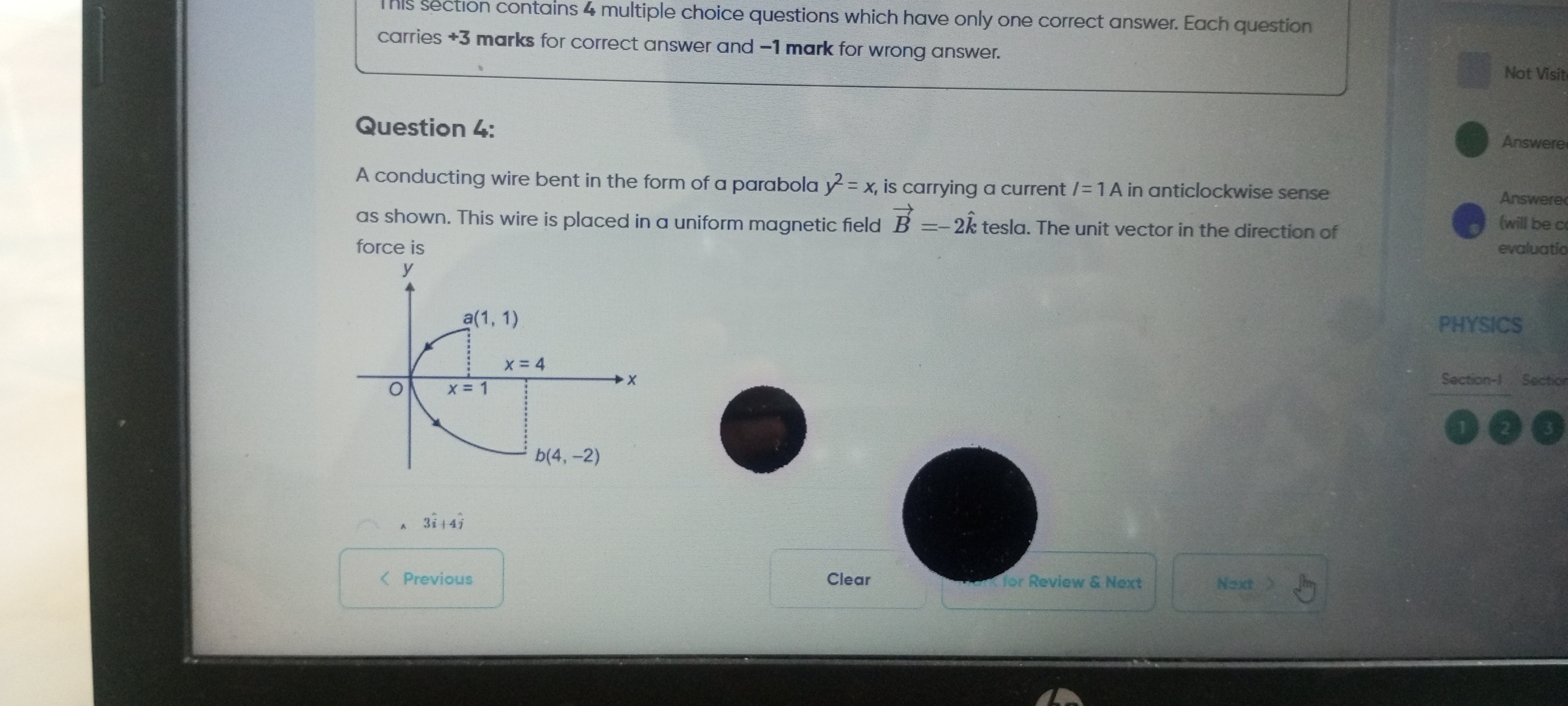
• A. $3\hat{i} + 4\hat{j}$

Answer 1

$\frac{\hat{i} + 2\hat{j}}{\sqrt{5}}$

Answer 2

The magnetic force on a current-carrying wire in a uniform magnetic field is $\vec{F} = I (\vec{L} \times \vec{B})$. The effective displacement vector $\vec{L}$ for the wire segment from O(0,0) to b(4,-2) is $4\hat{i} - 2\hat{j}$. Given $I=1$ A and $\vec{B} = -2\hat{k}$ T.

Calculate the cross product: $\vec{L} \times \vec{B} = (4\hat{i} - 2\hat{j}) \times (-2\hat{k}) = -8(\hat{i} \times \hat{k}) + 4(\hat{j} \times \hat{k}) = -8(-\hat{j}) + 4(\hat{i}) = 4\hat{i} + 8\hat{j}$.

So, $\vec{F} = 1 \times (4\hat{i} + 8\hat{j}) = 4\hat{i} + 8\hat{j}$.

The unit vector in the direction of force is $\hat{F} = \frac{\vec{F}}{|\vec{F}|} = \frac{4\hat{i} + 8\hat{j}}{\sqrt{4^2 + 8^2}} = \frac{4\hat{i} + 8\hat{j}}{\sqrt{16+64}} = \frac{4\hat{i} + 8\hat{j}}{\sqrt{80}} = \frac{4\hat{i} + 8\hat{j}}{4\sqrt{5}} = \frac{\hat{i} + 2\hat{j}}{\sqrt{5}}$.