Question

This question has statement 1 and statement 2. Of the four choices given after the statements, choose the one that best describes the two statements. An insulating solid sphere of radius R has a uniformly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point outside the sphere. The electric potential at infinity is zero.
Statement-1: When a charge q is taken from the centre to the surface of the sphere, its potential energy changes by $\dfrac{q\rho }{3{{\varepsilon }_{0}}}$
Statement-2: The electric field at a distance r (rA. Statement-1 is true, statement-2 is true; statement-2 is not the correct explanation of statement-1.
B. statement-1 is true, statement-2 is false.
C. statement-1 is false, statement-2 is true.
D. statement-1 is true, statement-2 is true; statement-2 is not the correct explanation of statement-1.

Answer 1

You could begin by proving the statement-2. You will get an expression for the electric field at a distance r from the centre by using Gauss’s law and then compare it with that given in statement-2. Now you could substitute that expression in the expression of potential difference in terms of electric field and further substitute that potential difference in the expression of change in potential energy and check whether you get it same as that given in statement-1.
Formula used:
Gauss’s law,
$\int\limits_{s}{E}\bullet dA=\dfrac{1}{{{\varepsilon }_{0}}}{{Q}_{_{en}}}$
Expression for change in potential energy,
$\Delta U=q\Delta V$
Expression for change in potential,
$\Delta V=\int{E\bullet dr}$

Complete answer:
For statement-2

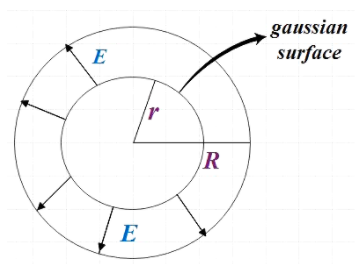
Let us consider a Gaussian surface at distance r (r$\int\limits_{s}{E}\bullet dA=\dfrac{1}{{{\varepsilon }_{0}}}{{Q}_{_{en}}}$
Since the given sphere is positively charged, we know that the electric field line will be radially outward as shown in the figure and the areal vector is also normal to the surface. Hence the angle between them is 0. So, $\int\limits_{s}{EdA\cos 0=\dfrac{1}{{{\varepsilon }_{0}}}}{{Q}_{en}}$
$E\int\limits_{s}{dA}=\dfrac{1}{{{\varepsilon }_{0}}}{{Q}_{en}}$ …………………….. (1)
But we know that Surface charge density (ρ) is given by,
$\rho =\dfrac{Q}{V}$
$Q=\rho V$ ………………………. (2)
Where, Q is the charge enclosed by the surface and V is the volume of the surface under consideration. The surface under consideration in the given question is that of a sphere, the volume here is the volume of a sphere given by,
$V=\dfrac{4}{3}\pi {{r}^{3}}$
Now (2) becomes
$Q=\rho \times \dfrac{4}{3}\pi {{r}^{3}}$ …………………. (3)
Also integrating$dA$ we get the surface area of the sphere which is given by,
$\int{dA=4\pi {{r}^{2}}}$ …………………… (4)
Substituting (3) and (4) in (1), we get,
$E\times \left( 4\pi {{r}^{2}} \right)=\dfrac{1}{{{\varepsilon }_{0}}}\left( \rho \times \dfrac{4}{3}\pi {{r}^{3}} \right)$
$\Rightarrow E=\dfrac{\rho r}{3{{\varepsilon }_{0}}}$
Therefore, the electric field at a distance r (rSo, the statement-2 is true.
For statement-1
We know that the change in potential energy is given by,
$\Delta U=q\Delta V$ ………………………….. (5)
Here the charge is taken from centre to the surface, so, the potential difference is given by,
$\Delta V={{V}_{S}}-{{V}_{C}}$
We have the expression for potential difference as,
$\Delta V=\int{E\bullet dr}$ …………………….. (6)

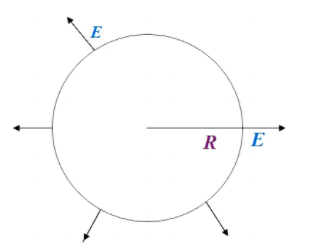
As the sphere is positively charged the electric field is directed radially outward and the radial vector $dR$ is also in the same direction. So the angle between them is 0. So (6) can be given as,
$\Delta V=\int\limits_{r=0}^{r=R}{EdR\cos 0=}\int\limits_{r=0}^{r=R}{EdR}$
But, the electric field at a distance r (rSubstituting, we get,
$\Rightarrow \Delta V=\int\limits_{0}^{R}{\left( \dfrac{\rho r}{3{{\varepsilon }_{0}}} \right)}dR$
$\Rightarrow \Delta V=\dfrac{\rho }{3{{\varepsilon }_{0}}}\left( \dfrac{{{r}^{2}}}{2} \right)_{0}^{R}$
$\Rightarrow \Delta V=\dfrac{\rho {{R}^{2}}}{6{{\varepsilon }_{0}}}$
Now from (5), the change in potential energy can be given by,
$\Rightarrow \Delta U=q\left( \dfrac{\rho {{R}^{2}}}{6{{\varepsilon }_{0}}} \right)$
Therefore, when a charge q is taken from the centre to the surface of the sphere, its potential energy changes by $\dfrac{\rho q{{R}^{2}}}{6{{\varepsilon }_{0}}}$
So the statement-1 is false.
Therefore, statement-1 is false, statement-2 is true.

Hence the answer to the question is option C.

Note:
Though in the above solution we have begun proving the statement-2 true and then using the electric field derived there in proving statement-1, you could actually begin from statement-1. You could separately find the potential at centre and then at the surface and hence the potential difference between those points and then substitute to get the change in potential energy. So, you shouldn’t necessarily depend on the proof of statement-2 to prove statement-1.