Question

Thirteen resistances each of resistance $R \Omega$ are connected in the circuit as shown in the figure. The effective resistance between A and B is?

A) $\dfrac{{4R}}{3} \Omega$
B) $2R \Omega$
C) $R \Omega$
D) $\dfrac{{2R}}{3} \Omega$

Answer 1

Note that the circuit is symmetrical. Hence, the potential difference across the central resistor is zero, and the circuit can be treated as a balance wheatstone bridge. The resistors of this wheat stone bridge will be the equivalent resistance of the small triangle configuration units formed at the corners.

Formula used:
If two resistors ${R_1}$ and ${R_2}$ are connected in series, the equivalent resistance is given by ${R_{eq}} = {R_1} + {R_2}$.
If two resistors ${R_1}$ and ${R_2}$ are connected in parallel, the equation for equivalent resistance becomes
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
$\Rightarrow {R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$

Complete step by step solution:
Thirteen resistances each of resistance $R \Omega$ are connected in the circuit as shown in the following figure.

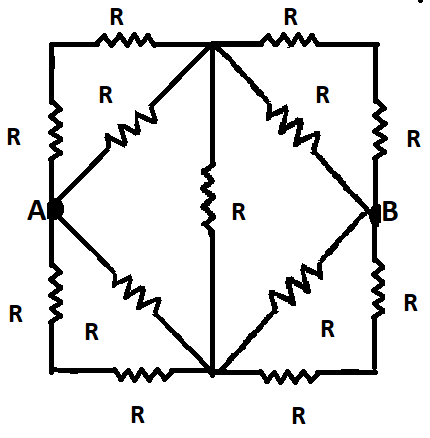
Now, note that the circuit is symmetrical. Hence, the potential difference across the central resistor is zero, and the circuit can be treated as a balance wheatstone bridge.
The resistors of this wheat stone bridge will be the equivalent resistance of the small triangle configuration units formed at the corners.

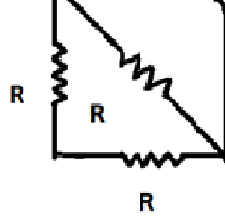
Now, the effective resistance will be the same as the resistance of a single triangular unit. Here in each triangular unit, two resistors are in series and the other one is connected in parallel.
We know, if two resistors ${R_1}$ and ${R_2}$ are connected in series, the equivalent resistance is given by ${R_{eq}} = {R_1} + {R_2}$. When they are connected in parallel, the equivalent resistance $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ $\Rightarrow {R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$
So, effective resistance = $\dfrac{{\left( {R + R} \right) \times R}}{{\left( {R + R} \right) + R}} = \dfrac{{2{R^2}}}{{3R}} = \dfrac{{2R}}{3}$ $\Omega$
Therefore, the effective resistance between A and B is $\dfrac{{2R}}{3}$ $\Omega$.

Hence, the correct answer is option (D).

Note: The circuit is symmetrical. So, the potential difference across the central resistor is zero and the circuit can be treated as a balance wheatstone bridge. Hence, the effective resistance of the wheatstone bridge will be the same as the resistance of a single triangular unit.