Question

There is –ve charge $q$ as shown in the figure. Take the potential to be zero at infinity. If $A$ and $B$ are two points in the charge’s vicinity, then the potential at –

$(A)$ $A$ is less than $B$
$(B)$ $A$ s more than that at $B$
$(C)$ $A$ is greater in magnitude than at $B$
$(D)$ $A$ is smaller in magnitude than at $B$

Answer 1

First, the potentials have to be calculated for the two points. To do so, the distances have to be assumed from the charge to the points. And, by using the formula of electrical potential the potentials at point A and point B can be found. Since the potential is inversely proportional to the distance, the comparison of potential between two points can be easily understood. Note that, the sign of the potential equally matters as the magnitude.
Formula used:
Electric potential, $V = k\dfrac{Q}{R}$
Where, $Q$ is the charge, $R$ is the distance and, $k$ is a constant term.

Complete step-by-step solution:

Noticing the above diagram it is necessary to modify it by assuming the distances from the charge to the points, such as:

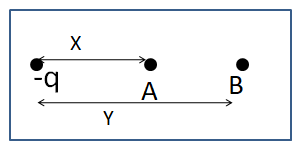
Let, the distance from the charge to the point $A$ is $X$ and the distance from the charge to the point $B$ is $Y$.
Now using the formula of electrical potential i.e Electric potential, $V = k\dfrac{Q}{R}$
Where, $Q$ is the charge, $R$ is the distance and, $k$ is a constant term.
For the point $A$,
$Q = - q$
$R = X$
$\therefore {V_A} = - \dfrac{{kq}}{X}$
For the point $B$,
$Q = - q$
$R = Y$
$\therefore {V_B} = - \dfrac{{kq}}{{Y}}$
Since the potential is inversely proportional to the distance, and here we can see $Y > X$
We may write the magnitude of potential at point $A$ is greater than point $B$.
But, the sign of potential is very important. And, due to the negative sign convention potential at point $B$ is larger than that of at point $A$
Hence here we find two correct options:
$(A)$ $A$ is less than $B$
And, $(C)$ $A$ is greater in magnitude than at $B$

Note: The Electric potential is the amount of work that is needed to move a unit charge from a reference point to a certain point against an electric field. Generally, the reference point is Earth, but any point beyond the effect of the electric field can be used.
A positive potential means that the charge of the effective particle is the same as the charge of the affected particle. Since the same charges repel, the work-done against the forces between the charges to bring them closer.
A negative potential means that the charge of the effective particle is the opposite of the affected particle. Since the different charges attract, they don't need external work to bring them closer.