Question
Question: There is an infinite wire grid with cells in the form of equilateral triangles. The resistance of ea...
There is an infinite wire grid with cells in the form of equilateral triangles. The resistance of each wire between neighbouring joint connections is R0. The net resistance of the whole grid between the points A and B as shown is:
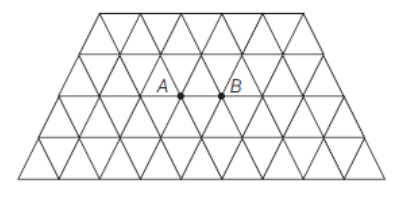
a. R0
b. 2R0
c. 3R0
d. 4R0
Solution
To answer this question we need to know the concept of the superposition theorem. The superposition principle states that in case there are two or more than two waves that will overlap in the space, the sum of the resultant disturbance from the overlapping will be similar to that of the algebraic sum of the overlapping waves considered individually.
Complete step by step answer:
First let us consider if ‘I’ amount of current enters at ‘A’. Then we can write that:
6I will flow through AB.
Now, in the second case, let the current be extracted from B, again current 6I will flow through AB.
Now, if simultaneously current enters at A and leaves at B, then the current 6I+61=3I should flow through AB.
Now we can write that the current will be: I−3I=32I that will flow through the remaining part.
Now, let us consider the resistance of the remaining part will be: R1
Hence, the expression that can be formed is:
Now 3R0I=3R12I
R0=2R1
Hence the expression is formed as:
Req=R1+R0R1R0
=R1+2R1R12R1
After the evaluation we obtain the final expression as:
=32R1
=3R0
Hence, the correct answer is option (C).
Note: We should keep in mind that in order to calculate the total amount of current in any part of the linear circuit which will be equal to that of the algebraic sum of all the currents that will be formed in each of the sources that is considered separately. The separate currents are to be combined and then replaced with specific voltage sources by all the short circuits and then every other current source will be replaced by open circuits.
