Question

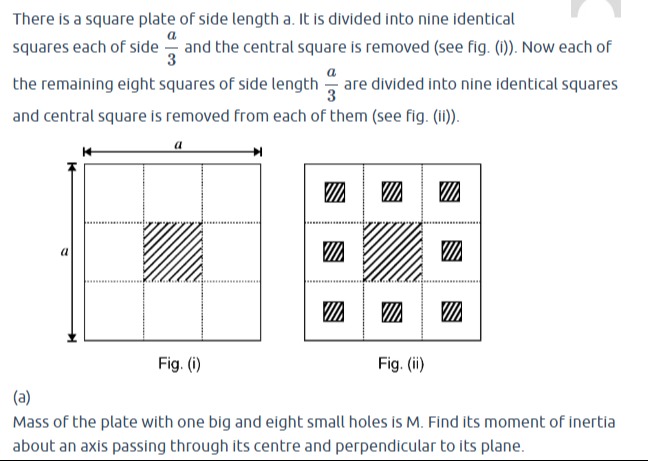
There is a square plate of side length a. It is divided into nine identical squares each of side $\frac{a}{3}$ and the central square is removed (see fig. (i)). Now each of the remaining eight squares of side length $\frac{a}{3}$ are divided into nine identical squares and central square is removed from each of them (see fig. (ii)).

Answer 1

The moment of inertia of the plate with one big and eight small holes about an axis passing through its centre and perpendicular to its plane is $\frac{91 M a^2}{486}$.

Answer 2

The problem asks for the moment of inertia of a square plate with a specific pattern of holes about an axis passing through its center and perpendicular to its plane. We will use the principle of superposition. The moment of inertia of the plate with holes is the moment of inertia of the original solid plate minus the moment of inertia of the removed parts.

Let the side length of the original square plate be $a$.
Let the mass of the original solid square plate be $M_0$.
The moment of inertia of a solid square plate of mass $m$ and side length $L$ about an axis through its center and perpendicular to its plane is given by $I = \frac{mL^2}{6}$.
So, the moment of inertia of the original solid plate is $I_{total} = \frac{M_0 a^2}{6}$.

Step 1: Removing the central square (Fig. i)

A central square of side length $a/3$ is removed.
Area of this removed square = $(a/3)^2 = a^2/9$.
Since the mass is uniformly distributed, the mass of this removed square, $m_1$, is:
$m_1 = M_0 \times \frac{\text{Area of removed square}}{\text{Area of original plate}} = M_0 \times \frac{a^2/9}{a^2} = \frac{M_0}{9}$.
The center of this removed square coincides with the center of the original plate.
So, its moment of inertia about the central axis is:
$I_1 = \frac{m_1 (a/3)^2}{6} = \frac{(M_0/9) (a^2/9)}{6} = \frac{M_0 a^2}{486}$.

Step 2: Removing small central squares from the remaining eight squares (Fig. ii)

Each of the remaining 8 squares has a side length of $a/3$. From each of these, a central square is removed.
The side length of these smaller removed squares is $(a/3)/3 = a/9$.
The mass of each of these 8 small removed squares, $m_s$, is:
$m_s = M_0 \times \frac{\text{Area of small removed square}}{\text{Area of original plate}} = M_0 \times \frac{(a/9)^2}{a^2} = \frac{M_0}{81}$.

We need to find the moment of inertia of these 8 small removed squares about the central axis of the original plate. We use the parallel axis theorem: $I = I_{CM} + md^2$, where $I_{CM}$ is the moment of inertia about the square's own center, $m$ is its mass, and $d$ is the distance from its center to the overall central axis.
The moment of inertia of each small removed square about its own center is:
$I_{CM,s} = \frac{m_s (a/9)^2}{6} = \frac{(M_0/81) (a^2/81)}{6} = \frac{M_0 a^2}{39366}$.

The centers of the 8 small removed squares are located at the centers of the 8 outer $a/3$ squares.
These 8 squares are of two types:

1. Four squares whose centers are at $(\pm a/3, 0)$ and $(0, \pm a/3)$ relative to the overall center. For these, the distance $d_1 = a/3$.
   Moment of inertia for each of these 4 squares about the central axis:
   $I_{s1} = I_{CM,s} + m_s d_1^2 = \frac{M_0 a^2}{39366} + \frac{M_0}{81} \left(\frac{a}{3}\right)^2 = \frac{M_0 a^2}{39366} + \frac{M_0 a^2}{729}$
   $I_{s1} = M_0 a^2 \left( \frac{1}{39366} + \frac{54}{39366} \right) = \frac{55 M_0 a^2}{39366}$.
   Total for these 4 squares: $4 \times I_{s1} = \frac{220 M_0 a^2}{39366}$.

2. Four squares whose centers are at $(\pm a/3, \pm a/3)$ relative to the overall center. For these, the distance $d_2 = \sqrt{(a/3)^2 + (a/3)^2} = \frac{\sqrt{2}a}{3}$.
   Moment of inertia for each of these 4 squares about the central axis:
   $I_{s2} = I_{CM,s} + m_s d_2^2 = \frac{M_0 a^2}{39366} + \frac{M_0}{81} \left(\frac{\sqrt{2}a}{3}\right)^2 = \frac{M_0 a^2}{39366} + \frac{2 M_0 a^2}{729}$
   $I_{s2} = M_0 a^2 \left( \frac{1}{39366} + \frac{108}{39366} \right) = \frac{109 M_0 a^2}{39366}$.
   Total for these 4 squares: $4 \times I_{s2} = \frac{436 M_0 a^2}{39366}$.

The total moment of inertia of all 8 small removed squares is:
$I_2 = \frac{220 M_0 a^2}{39366} + \frac{436 M_0 a^2}{39366} = \frac{656 M_0 a^2}{39366}$.

The moment of inertia of the final plate (with holes) is $I_{final} = I_{total} - I_1 - I_2$.
$I_{final} = \frac{M_0 a^2}{6} - \frac{M_0 a^2}{486} - \frac{656 M_0 a^2}{39366}$.
To combine these, find a common denominator, which is $39366$.
$\frac{1}{6} = \frac{6561}{39366}$
$\frac{1}{486} = \frac{81}{39366}$
$I_{final} = M_0 a^2 \left( \frac{6561 - 81 - 656}{39366} \right) = M_0 a^2 \left( \frac{5824}{39366} \right)$.

Finally, we are given that the mass of the plate with holes is $M$. We need to express $I_{final}$ in terms of $M$.
The total mass removed is $m_1 + 8 \times m_s$:
$M_{removed} = \frac{M_0}{9} + 8 \times \frac{M_0}{81} = \frac{9 M_0}{81} + \frac{8 M_0}{81} = \frac{17 M_0}{81}$.
The mass of the plate with holes, $M$, is:
$M = M_0 - M_{removed} = M_0 - \frac{17 M_0}{81} = M_0 \left( 1 - \frac{17}{81} \right) = M_0 \left( \frac{81 - 17}{81} \right) = \frac{64 M_0}{81}$.
From this, we can express $M_0$ in terms of $M$: $M_0 = \frac{81 M}{64}$.

Substitute $M_0$ into the expression for $I_{final}$:
$I_{final} = \frac{5824}{39366} \times \frac{81 M}{64} a^2$.
Simplify the numerical fraction:
$\frac{5824}{39366} = \frac{2912}{19683}$.
$19683 = 81 \times 243$.
So, $I_{final} = \frac{2912}{81 \times 243} \times \frac{81 M}{64} a^2 = \frac{2912 M a^2}{243 \times 64}$.
Simplify $\frac{2912}{64}$:
$2912 \div 64 = 45.5$. This means $2912/64 = 91/2$.
So, $I_{final} = \frac{91/2 M a^2}{243} = \frac{91 M a^2}{486}$.

The final answer is $\frac{91Ma^2}{486}$.

Explanation of the solution:

1. Identify the base shape and its properties: Start with a solid square plate of side 'a' and assume its mass is $M_0$. Calculate its moment of inertia about the central axis.
2. Apply Superposition Principle: The moment of inertia of the plate with holes is found by subtracting the moment of inertia of the removed parts from the moment of inertia of the original solid plate.
3. Calculate Moment of Inertia of Removed Parts (Level 1): The first removed part is a central square of side $a/3$. Calculate its mass ($m_1$) and its moment of inertia ($I_1$) about the overall central axis (which passes through its own center).
4. Calculate Moment of Inertia of Removed Parts (Level 2): Eight smaller squares of side $a/9$ are removed. Calculate the mass of each ($m_s$). Use the parallel axis theorem ($I = I_{CM} + md^2$) for each of these 8 squares, as their centers are offset from the overall central axis. Sum the moments of inertia for all 8 squares ($I_2$).
5. Total Moment of Inertia: Subtract $I_1$ and $I_2$ from the initial $I_{total}$ to get $I_{final}$ in terms of $M_0$.
6. Relate $M_0$ to $M$: Calculate the total mass removed ($M_{removed} = m_1 + 8m_s$). The given mass $M$ is $M_0 - M_{removed}$. Express $M_0$ in terms of $M$.
7. Substitute and Simplify: Substitute the expression for $M_0$ into $I_{final}$ and simplify the resulting expression.