Question

There is a spherical glass shell of refractive index 1.5, inner radius 10 cm and outer radius 20 cm. inside the spherical cavity, there is air. A point object is placed at a point O at a distance of 30 cm from the outer spherical surface. Find the final position of the image as seen by the eye.

(A) $11.75cm$ from center
(B) $28.75cm$ from center
(C) $78.75cm$ from center
(D) $18.75cm$ from center

Answer 1

Hint
The question is based on the virtual image of the convex lens. We will make use of the refraction through the convex lens formula, as our eye is considered to be convex.
In this solution we will be using the following formulas,
$\Rightarrow \dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R}$
Where ${n_1}$ and ${n_2}$ are the refractive indices of air and glass
$v$ is the image distance and $u$ is the object distance
$R$ is the radius of the sphere.

Complete step by step answer
To calculate the virtual image we can use the following formula,
$\Rightarrow \dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R}$……. (1)
We can see from the diagram given that there are 4 surfaces. And they are ${S_1}$, ${S_2}$, ${S_3}$ and ${S_4}$.

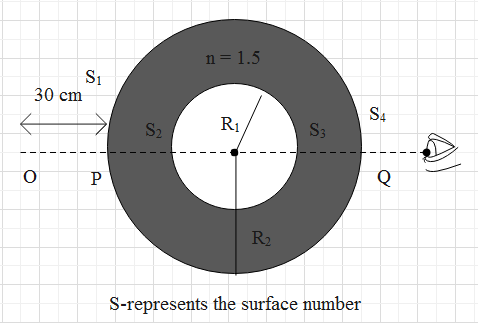
Let us consider the first surface. So here the ${n_1}$ will be 1 and ${n_2}$ is given as $1.5$. According to the question the object is placed at O so $u$ is $30cm$. And the radius of the sphere whose surface is ${S_1}$ is given $20cm$.
So by substituting these values in the equation (1) we get
$\Rightarrow \dfrac{{1.5}}{v} - \dfrac{1}{{ - 30}} = \dfrac{{1.5 - 1}}{{20}}$
From here to find $v$ we take all the other terms to the RHS
$\dfrac{{1.5}}{v} = \dfrac{{0.5}}{{20}} - \dfrac{1}{{30}}$
On taking LCM as 60,
$\Rightarrow \dfrac{{1.5}}{v} = \dfrac{{1.5 - 2}}{{60}}$
On taking reciprocal and keeping only $v$ in the LHS,
$\Rightarrow v = - \dfrac{{60}}{{0.5}} \times 1.5$
On calculating this gives the image distance for ${S_1}$ as $v = - 180cm$
Now let us consider the second surface ${S_2}$.
The object distance will be, $- 180 + ( - 10) = - 190\,cm$ and now the ${n_1}$ will be $1.5$ and ${n_2}$ will be 1. The radius will be of the smaller sphere, that is $10cm$
So substituting the values in the equation (1)
$\Rightarrow \dfrac{1}{v} - \dfrac{{1.5}}{{ - 190}} = \dfrac{{1 - 1.5}}{{10}}$
From here to find $v$ we take all the other terms to the RHS
$\dfrac{1}{v} = \dfrac{{ - 0.5}}{{10}} - \dfrac{{1.5}}{{190}}$
On taking LCM as 190,
$\Rightarrow \dfrac{1}{v} = \dfrac{{ - 9.5 - 1.5}}{{190}}$
On taking reciprocal,
$\Rightarrow v = - \dfrac{{190}}{{11}}cm$
Let us now consider the third surface ${S_3}$.
The object distance will be, $- \dfrac{{190}}{{11}} + ( - 20) = - \dfrac{{410}}{{11}}\,cm$. Again here the ${n_1}$ will be 1 and ${n_2}$ is given as $1.5$. And the radius of the sphere whose surface is ${S_3}$ and is given $10cm$.
By substituting the values in the equation (1) we get
\Rightarrow \dfrac{{1.5}}{v} - \dfrac{1}{{ - {\raise0.7ex\hbox{{410}} \\!\mathord{\left/ {\vphantom {{410} {11}}}\right.} \\!\lower0.7ex\hbox{{11}}}}} = \dfrac{{1.5 - 1}}{{ - 10}}
We can write this as,
$\Rightarrow \dfrac{{1.5}}{v} = - \dfrac{{0.5}}{{10}} - \dfrac{{11}}{{410}}$
On taking LCM as 140,
$\Rightarrow \dfrac{{1.5}}{v} = \dfrac{{ - 20.5 - 11}}{{410}}$
On taking reciprocal and keeping only $v$ in the LHS,
$\Rightarrow v = - \dfrac{{410}}{{21}}cm$
Finally for the fourth surface, ${S_4}$
The object distance will be, $- \dfrac{{410}}{{21}} + ( - 10) = - \dfrac{{620}}{{21}}\,cm$, ${n_1}$ will be $1.5$ and ${n_2}$ will be 1. And radius will be $20cm$
Substituting the values in the equation (1) we get,
\Rightarrow \dfrac{1}{v} - \dfrac{{1.5}}{{ - {\raise0.7ex\hbox{{620}} \\!\mathord{\left/ {\vphantom {{620} {21}}}\right.} \\!\lower0.7ex\hbox{{21}}}}} = \dfrac{{1 - 1.5}}{{ - 20}}
From here to find $v$ we take all the other terms to the RHS
$\dfrac{1}{v} = \dfrac{{0.5}}{{20}} - \dfrac{{1.5 \times 21}}{{620}}$
On taking LCM as 620,
$\Rightarrow \dfrac{1}{v} = \dfrac{{15.5 - 31.5}}{{620}}$
On taking reciprocal
$\Rightarrow v = - 38.75cm$
To find the distance from the center we subtract it by the radius of the larger sphere, 20cm,
Hence we get $\left( {38.75 - 20} \right)cm = 18.75cm$
Therefore, the final position of the image as seen by the eye is 18.75 cm.
Thus, option (D) is correct.

Note
Here we have taken the positive sign for the distances that are measured from the center towards the left and negative for all the distances from the center towards the right. This assigning of negative or positive value of the sign convention helps us to understand the direction of where the image is formed with respect to the center.