Solveeit Logo
Login

Question

Question: There is a point inside a circle, what is the probability that this point is closer to the circumfer...

There is a point inside a circle, what is the probability that this point is closer to the circumference than to the centre?
A. 34\dfrac{3}{4}
B. 12\dfrac{1}{2}
C. 14\dfrac{1}{4}
D. 13\dfrac{1}{3}

Explanation

Solution

Circumference of the circle or perimeter of the circle is the measurement of the boundary of the circle. Whereas the area of the circle defines the region occupied by it. Area of any circle is the region enclosed by the circle itself or the space covered by the circle. The formula to find the area of the circle is = πr2\pi {r^2} and for point to be close to the circumference than to the centre the point must be at a distance greater than r2\dfrac{r}{2} from the centre of circle.

Complete step by step solution:
Total possible outcomes = Area of circle = πr2\pi {r^2}
And let the radius of the circle be 'r'. Observe the figure, we have to find the probability of point, P in the ring which will be closer to circumference. For point to be close to the circumference than to the centre the point must be at a distance greater than r2\dfrac{r}{2} from the centre of circle where r is the radius, in which in the figure r=r2r = \dfrac{r}{2}.

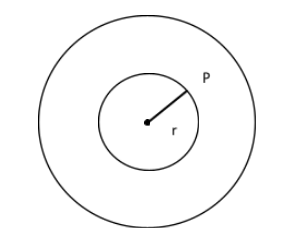
Area of ring = Area of outer circle - Area of inner circle
Area of ring = πr2−π(r2)2\pi {r^2} - \pi {\left( {\dfrac{r}{2}} \right)^2}
Area of ring= πr2−πr24\pi {r^2} - \dfrac{{\pi {r^2}}}{4}
Therefore, the outcome is 3πr24\dfrac{{3\pi {r^2}}}{4}.
Area of region of a point such that distance is greater than r2\dfrac{r}{2} from the centre of circle = 3πr24\dfrac{{3\pi {r^2}}}{4}
Hence, the Probability that this point is close to the circumference than to the centre is
3πr24πr2\dfrac{{\dfrac{{3\pi {r^2}}}{4}}}{{\pi {r^2}}} = 34\dfrac{3}{4}

Therefore, option A is the right answer.

Note: The key point to find the probability in which the point is close to the circumference than to the centre, we can consider the area of the region of the point with respect to area of circle and the distance surrounding a circle is known as the circumference of the circle. The diameter is the distance across a circle through the centre, and it touches the two points of the circle perimeter.