Question

There is a horizontal film of soap solution. On it a thread is placed in the form of a loop. The film is punctured inside the loop and the thread becomes a circular loop of radius $R$. If the surface tension of the soap solution be $T$, then the tension in the thread will be
A. $\dfrac{{\pi {R^2}}}{T}$
B. $\pi {R^2}T$
C. $2\pi RT$
D. $2RT$

Answer 1

Consider the small arc of the thread in the circular loop. Determine the expression for the surface tension of the soap solution on this thread arc and the tension experienced by the thread in the opposite direction to that of the tension due to the soap solution. Thus, derive an expression for the tension in the thread.

Formula used:
The arc $s$ of cone is given by
$s = R\theta$ …… (1)
Here, $R$ is the radius of the cone and $\theta$ is the angle subtended by the cone.

Complete step by step answer:
We have given that the thread placed on the horizontal film of soap solution forms a loop. But when the film is punctured inside the loop, the thread forms a circular loop of radius $R$. The surface tension of the soap solution is $T$. Let us consider a small arc of the circular loop formed by the thread when the film is punctured.

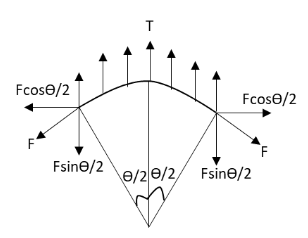
In the above figure, $\theta$ is the angle subtended by the small cone, $T$ is the surface tension in the soap solution and $T'$ is the tension experienced by the thread. The components of the tension experienced by the thread are shown in the above diagram.The total tension exerted by the soap solution film on the small length $\Delta l$ of the thread is $2T\Delta l$.

This tension exerted by the soap solution is balanced by the vertical component of the surface tension experienced by the thread.
$2T\Delta l = 2F\sin \dfrac{\theta }{2}$
$\Rightarrow T\Delta l = F\sin \dfrac{\theta }{2}$
The angle in the above equation is very small. Hence, the above equation becomes.
$\Rightarrow T\Delta l = F\dfrac{\theta }{2}$
According to equation (1), substitute $R\theta$ for $\Delta l$ in the above equation.
$\Rightarrow TR\theta = F\dfrac{\theta }{2}$
$\therefore F = 2RT$
Therefore, the tension in the thread will be $2RT$.

Hence, the correct option is D.

Note: One can also show that the tension due to the soap solution is balanced by the vertical component of the tension experienced by the thread by using Newton’s second law of motion as the thread is in a steady state when it forms a circular loop. One should always remember that the angle subtended by the arc of the thread is very small, so sine of angle is equal to angle.