Question
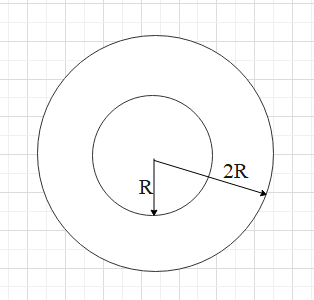
Question: There is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portion...
There is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portion is M. What is the gravitational potential at the centre?
A. 7R−5GM
B. 14R−7GM
C. 7R−3GM
D. 14R−9GM
Solution
Formula for gravitational potential have been used. We will consider a circle of the same radius as that of the cavity with negative mass that can fill the sphere. After calculating the potential for both spheres we will get the gravitational potential at center.
Formula used:
Mass = Volume × Density
v=2R−3GM
Complete step by step answer:
We have a sphere shell with inner radius R and outer radius 2R. The leftover mass between the two circles is M. We have to calculate the gravitational potential at the center.
For any solid sphere the potential at the center is given by
v=2R−3GM
As we have to find potential and there is a cavity in the center. Let us assume that we fill the cavity with a sphere having negative mass that can fill the sphere. Let us calculate the density be and we know formula of solid sphere will be
