Question

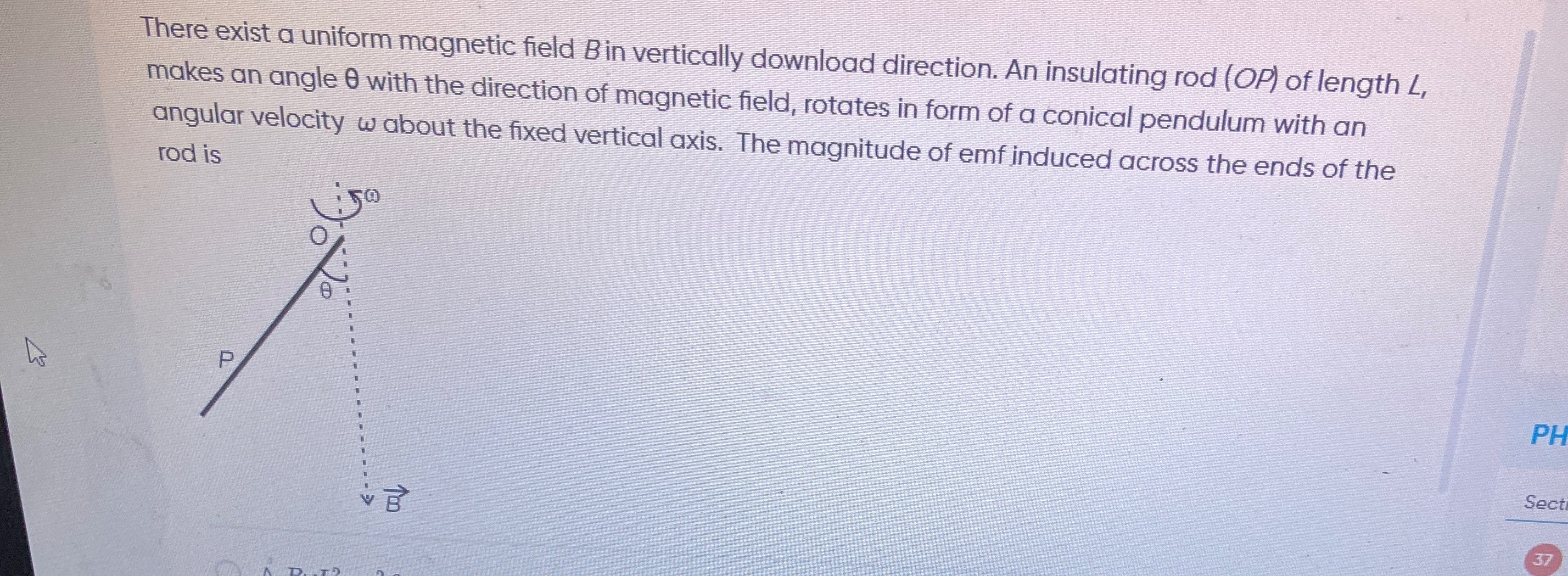
There exist a uniform magnetic field $B$ in vertically download direction. An insulating rod ($OP$) of length $L$, makes an angle $\theta$ with the direction of magnetic field, rotates in form of a conical pendulum with an angular velocity $\omega$ about the fixed vertical axis. The magnitude of emf induced across the ends of the rod is

• A. $\frac{1}{2} B \omega L^2 \sin^2\theta$

Answer 1

Answer: (A)

$\frac{1}{2} B \omega L^2 \sin^2\theta$

Answer 2

The rod $OP$ of length $L$ rotates with angular velocity $\omega$ about a fixed vertical axis. The rod makes an angle $\theta$ with the vertical. A uniform magnetic field $\vec{B}$ is directed vertically downwards.

Consider an elementary length $dr$ of the rod at a distance $r$ from the fixed end $O$. The radius of the horizontal circular path traced by this elementary length is $R_r = r \sin\theta$. The velocity of this elementary length is $\vec{v}$, which is tangential to its circular path and lies in the horizontal plane. The magnitude of the velocity is $v = \omega R_r = \omega r \sin\theta$. The magnetic field $\vec{B}$ is vertically downwards. Since $\vec{v}$ is in the horizontal plane and $\vec{B}$ is vertical, $\vec{v}$ is perpendicular to $\vec{B}$.

The induced EMF across the elementary length $dr$ is $d\mathcal{E} = (\vec{v} \times \vec{B}) \cdot d\vec{l}$. The vector $\vec{v} \times \vec{B}$ is in the horizontal plane. The elementary length vector $d\vec{l}$ has a horizontal component $dr \sin\theta$ and a vertical component $dr \cos\theta$. Since $\vec{v} \times \vec{B}$ is horizontal, only the horizontal component of $d\vec{l}$ contributes to the dot product. The magnitude of $(\vec{v} \times \vec{B})$ is $vB = (\omega r \sin\theta) B$. The direction of $(\vec{v} \times \vec{B})$ is perpendicular to $\vec{v}$ and $\vec{B}$. It will be in the horizontal plane, pointing radially outwards or inwards depending on the rotation direction. The horizontal component of $d\vec{l}$ is $dr \sin\theta$ and points radially outwards from the axis of rotation. Thus, $(\vec{v} \times \vec{B})$ and the effective $d\vec{l}$ (horizontal component) are parallel (or anti-parallel). So, $d\mathcal{E} = (\omega r \sin\theta) B (dr \sin\theta) = \omega B r \sin^2\theta dr$.

To find the total induced EMF across the ends of the rod, we integrate $d\mathcal{E}$ from $r=0$ to $r=L$:

$$\mathcal{E} = \int_0^L \omega B r \sin^2\theta dr$$ $$\mathcal{E} = \omega B \sin^2\theta \int_0^L r dr$$ $$\mathcal{E} = \omega B \sin^2\theta \left[ \frac{r^2}{2} \right]_0^L$$ $$\mathcal{E} = \omega B \sin^2\theta \left( \frac{L^2}{2} \right)$$ $$\mathcal{E} = \frac{1}{2} B \omega L^2 \sin^2\theta$$

The magnitude of the emf induced across the ends of the rod is $\frac{1}{2} B \omega L^2 \sin^2\theta$.