Question

There are two temples, one on each bank of a river just opposite to each other. One temple is 54m high from the top of this temple, the angles of depression of the top and the foot of the other temple are ${30^0}$and ${60^0}$respectively find the width of the river and the height of the other temple in meters.

Answer 1

The angle made between the two points with the horizontal is known to be the angle of depression or the angle of elevation according to the need of the question. We will take here trigonometric ratio $\cot$ for${60^0}$ and $\tan$for ${30^0}$. We will then subtract the height from the top of the small temple to the top of the big temple.

Complete step-by -step solution:
The angles of depression of the top and the foot of the other temple are ${30^0}$, and${60^0}$respectively, and the height of one temple is 54 meters.
According to the question, following rough sketch is drawn:

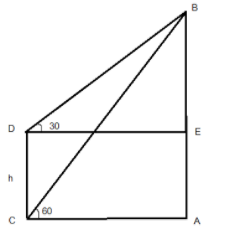
Now, let AB and CD be the two temples and AC be the river.
Consider the width of the river to be $x$.
$AB = 54m,{\text{ }}AC = x,{\text{ }}CD = h,\angle EDB = {30^0},\angle ACB = {60^0}$
From the triangle ABC:

$$\Rightarrow \dfrac{{AC}}{{AB}} = \cot {60^0} = \dfrac{1}{{\sqrt 3 }} \\\ \Rightarrow AC = \dfrac{{54}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }} = 18\sqrt 3 m - - - - (i) \\\$$

$DE = AC = 18\sqrt 3 m$
Again in triangle BDE:

$$\Rightarrow \dfrac{{BE}}{{DE}} = \tan {30^0} = \dfrac{1}{{\sqrt 3 }} \\\ \Rightarrow BE = \left( {18\sqrt 3 \times \dfrac{1}{{\sqrt 3 }}} \right) \\\ = 18m \\\$$

From the figure:

$$\Rightarrow CD = AE = AB - BE \\\ \Rightarrow CD = AE = (54 - 18)m = 36m \\\$$

Hence, the width of the river is $18\sqrt 3$ meters and the height of the smaller temple is 18 meters.

Hence the correct answer is option C

Note: In these types of height and distance problems, we should first draw the figure. Then as per requirement, we will choose the angle and relate it with the trigonometric ratio. Find the correlation between the known values and unknown values asked. Remember the general formula about the opposite side, adjacent and hypotenuse properties for all the trigonometric functions along with the trigonometric table for the reference values.