Question

There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. As observed from the top of this temple, the angle of depression of the top and the foot of the other temple are ${{30}^{\circ }}$ and ${{45}^{\circ }}$ respectively. Find the width of the river and the height of the other temple.

Answer 1

To solve this question we will use concept of tangent in triangle, which is
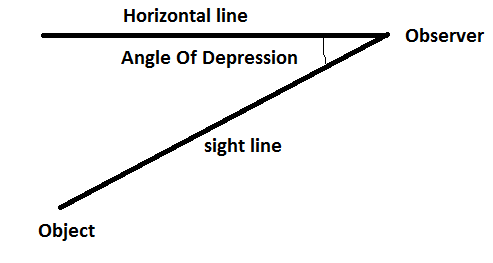
$\tan \theta =\dfrac{Perpendicular}{\text{Base}}$ . In this question, we will first apply the tangent formula that is mentioned above in both triangles $\Delta AOC$ and $\Delta BDC$ . Then, we will substitute the value of any one variable and hence, we will get the height of the temple as well as the width of the river. Also, in this type of question, one must also know about the angle of depression which is as follows. The term angle of depression denotes the angle from the horizontal downward to an object. An observer’s line of sight would be below the horizontal.

Complete step-by-step answer:
As mentioned in the question, the figure would look like the below picture

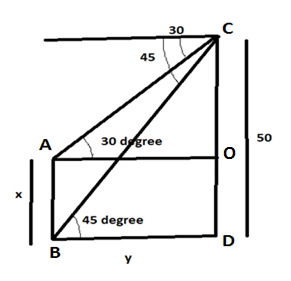
By inspecting the figure, we have
The height of temple CD which is given in the question is given as
=50m
Now, the angles of depression of the top and the bottom of the second temple are ${{30}^{\circ }}$ and ${{45}^{\circ }}$ .
Also, we know that
$\angle CAO={{30}^{\circ }}\ and\ \angle CBD={{45}^{\circ }}$
(Because of the property which is alternate interior angles are equal)

Let the height of the smaller temple be x m and the width of the river be y m.

Using the formula for tangent in the $\Delta AOC$ , we get

& \tan {{30}^{\circ }}=\dfrac{50-x}{y} \\\ & \dfrac{1}{\sqrt{3}}=\dfrac{50-x}{y} \\\ & x=50-\dfrac{y}{\sqrt{3}} \\\ \end{aligned}$$ Similarly, using the formula for tangent in the $$\Delta BDC$$ , we get $$\begin{aligned} & \tan {{45}^{\circ }}=\dfrac{50}{y} \\\ & 1=\dfrac{50}{y} \\\ & y=50 \\\ \end{aligned}$$ Now, using the value of y for finding x, we get $$\begin{aligned} & x=50-\dfrac{y}{\sqrt{3}} \\\ & x=50-\dfrac{50}{\sqrt{3}} \\\ & x=50\left( 1-\dfrac{1}{\sqrt{3}} \right) \\\ \end{aligned}$$ Hence, the width of the river is 50 m and the height of the second temple is $$50\left( 1-\dfrac{1}{\sqrt{3}} \right)$$ m. **Note:** The figure in this question is very tricky and is difficult to visualize it at first. Hence, the students can make an error while drawing the figure and then end up making a mistake and they would get to the correct solution. Also, in such questions, calculation mistakes are very common and to avoid them one must be extra careful while finding the solution.