Question

There are two poles on a horizontal plane. From the midpoint of the line joining their feet the tops of the poles appear at angles of elevation of $60^\circ$ and $30^\circ$. If the height of the first pole is 100 m then the height of the second is
A. $\dfrac{{100}}{3}$ m
B. $\dfrac{{100}}{7}$ m
C. $100\sqrt 3$ m
D. $\dfrac{{100}}{{\sqrt 3 }}$ m

Answer 1

Draw the line diagram. The angle of elevations of the tops of the poles is given. Let the distance between their feet be 2x meter. The height of one pole is given and from that, we will find the distance between the poles and the midpoint. Now we have the distance of the pole from the point of elevation and the angle of elevation, so using the formula for tangent i.e. $\tan \theta = \dfrac{{height}}{{base}}$, we will get the required value i.e. the height of the second pole.

Complete step by step answer:

Given that, there are two poles AB and CD on a horizontal plane.

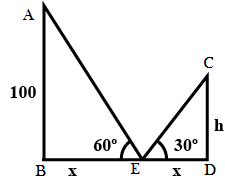
From the midpoint E of the line joining their feet, the tops of the poles appear at angles of elevation of $60^\circ$ and $30^\circ$.
$\Rightarrow \angle AEB = {60^ \circ }{\text{ and }}\angle CED = {30^ \circ }$
The height of the first pole is 100 m, i.e. AB = 100m
Let’s assume that the height of the other pole is h meter, and the distance between the two poles is given by 2x meters.
Now in $\Delta ABC$,
$\angle AEB = {60^ \circ }$ , AB=100 m, BE=x m
$\tan {60^ \circ } = \dfrac{{AB}}{{BE}}$
On substituting the value of $\tan {60^ \circ } = \sqrt 3$ , we get,
$\Rightarrow \dfrac{{100}}{x} = \sqrt 3$
On cross multiplication we get,
$\Rightarrow x = \dfrac{{100}}{{\sqrt 3 }}$
Again, in $\Delta CED$
$\angle CED = {30^ \circ }$ , DE= $x = \dfrac{{100}}{{\sqrt 3 }}$ m, CD=h m.
$\tan {30^ \circ } = \dfrac{h}{x}$
On substituting the values we get,
$\Rightarrow \dfrac{{h\sqrt 3 }}{{100}} = \dfrac{1}{{\sqrt 3 }}$
On simplification we get,
$\Rightarrow h = \dfrac{{100}}{{\sqrt 3 \times \sqrt 3 }}$
$\Rightarrow h = \dfrac{{100}}{3}$
Therefore, the height of the second pole is $\dfrac{{100}}{3}$ m.
Hence the correct option is (A).

Note: Most of the students get confused that the height of which of the pole is given that they get confused about the angle of elevation, so to overcome this problem we can use a simple method that As we know we have to look more upwards for a pole with greater height, and less upwards for a pole with a lower height.
Now we can see that the angle made by our eyes is the angle of elevation hence the pole with greater height should be having a greater angle of elevation, so we can clear our confusion by understanding this simple concept.
The trigonometric ratios of the standard angles are given by:

| ${0^ \circ }$| $30^\circ$| $45^\circ$| $60^\circ$| $90^\circ$
---|---|---|---|---|---
$\operatorname{Sin} {\text{ }}x$| 0| $\dfrac{1}{2}$| $\dfrac{1}{{\sqrt 2 }}$| $\dfrac{{\sqrt 3 }}{2}$| 1
$\operatorname{Cos} {\text{ }}x$| 1| $\dfrac{{\sqrt 3 }}{2}$| $\dfrac{1}{{\sqrt 2 }}$| $\dfrac{1}{2}$| 0
$\operatorname{Tan} {\text{ }}x$| 0| $\dfrac{1}{{\sqrt 3 }}$| 1| $\sqrt 3$| undefined
$Cot{\text{ }}x$| undefined| $\sqrt 3$| 1| $\dfrac{1}{{\sqrt 3 }}$| 0
$\operatorname{Cos} ec{\text{ }}x$| undefined| 2| $\sqrt 2$| $\dfrac{2}{{\sqrt 3 }}$| 1
$\operatorname{Sec} x$| 1| $\dfrac{2}{{\sqrt 3 }}$| $\sqrt 2$| 2| undefined