Question

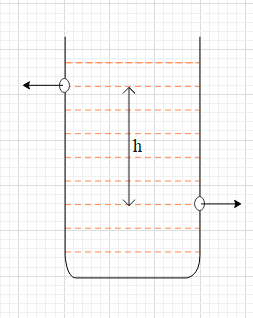
There are two identical small holes on the opposite sides of a tank containing a liquid. The tank is open at the top. The difference in height between two holes is h. As the liquid comes out of the two holes , the tank will experience a net horizontal force proportional to :

A. $\sqrt{h}$
B. $h$
C. ${{h}^{\dfrac{3}{2}}}$
D. ${{h}^{2}}$

Answer 1

Find the two velocities of the liquid at the two holes by using the formula for the velocity of efflux. Then find an expression for the change in momentum of the liquid at the hole in one second. The change in momentum in one second is force.

Formula used:
$v=\sqrt{2gH}$
$\rho =\dfrac{m}{V}$

Complete step by step answer:
Let the height of the bottommost hole from the base of the tank be x. Therefore, the height of the second hole is $(h+x)$.
The speed of the liquid coming out of a hole located at a height H from the base is given as $v=\sqrt{2gH}$, where g is acceleration due to gravity.
Let the speed of the liquid at the first hole be ${{v}_{1}}$. Therefore, ${{v}_{1}}=\sqrt{2gx}$.
Let the speed of the liquid at the second hole be ${{v}_{2}}$. Therefore, ${{v}_{2}}=\sqrt{2g(h+x)}$.
Suppose the liquid is coming out from a hole of area A, with the speed v. Then the volume of the liquid coming out of the hole in one second is equal to $V=vA$ …… (i).
Let the density of the liquid be $\rho$ and the mass coming out in one second be m.
We know that $\rho =\dfrac{m}{V}$.
Substitute the value of V from (i).
$\Rightarrow \rho =\dfrac{m}{vA}$
$\Rightarrow m=\rho vA$.
This means that the mass of the liquid coming out the hole in one second is $m=\rho vA$.
This also means that the change in momentum of the liquid in one second at the hole is $mv=(\rho vA)v=\rho {{v}^{2}}A$.
And the change in momentum in one second is the force (F) on the liquid.
$\Rightarrow F=\rho {{v}^{2}}A$
From Newton's third law of motion, we know that the liquid will exert a force equal to the magnitude to the force F but its direction is opposite to the direction of F.
Therefore, the force exerted on the tank is $F=\rho {{v}^{2}}A$.
Now, since the two holes are identical, the areas of both are the same.
Therefore, the force exerted on the tank at the first hole is ${{F}_{1}}=\rho v_{1}^{2}A$.
$\Rightarrow {{F}_{1}}=\rho {{\left( \sqrt{2gx} \right)}^{2}}A=2\rho gxA$
This force will be towards the left.
Similarly, the force on the tank at the second hole is ${{F}_{2}}=\rho v_{2}^{2}A=\rho {{\left( \sqrt{2g(h+x)} \right)}^{2}}A=2\rho gA(h+x)$.
The direction of this force is towards the right.
Since the two forces are opposite in direction, the net force on the tank is ${{F}_{net}}={{F}_{2}}-{{F}_{1}}$.
$\Rightarrow {{F}_{net}}=2\rho gA(h+x)-2\rho gAx=2\rho gAh$
From the above equation we get that the net force is proportional to the height h.

So, the correct answer is “Option B”.

Note:
To find the speeds of the liquid at the two holes we can also use Bernoulli's theorem, which relates the pressure and kinetic energy of the liquid at different points on the liquid. It is based on the law of conservation of energy.
The liquid will exert a force equal to the magnitude to the force F but its direction is opposite to the direction of F.