Question

There are two holes one each along the opposite sides of a wide rectangular tank. The cross-section of each hole is $0.01{\text{ }}{m^2}$ and the vertical distance between the holes is one meter. The tank is filled with water. The net force in the tank in Newton when water flows out of the holes is: (Density of water is $1000{\text{ }}\dfrac{{kg}}{{{m^3}}}$) ($g = 10{\text{ }}\dfrac{m}{{{s^2}}}$)
(i) $100$ (ii) $200$ (iii) $300$ (iv) $400$

Answer 1

We have to find the velocity of efflux of both the holes. Then we have to find the rate of flow of liquid from both the holes. We have to make use of the vertical distance as given in the question. From the derivative of momentum we will find the force.

Complete step-by-step solution:

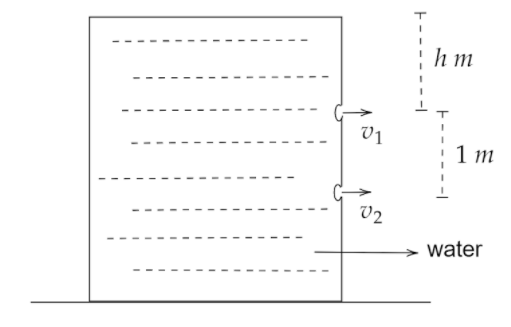
Velocity of efflux is defined as the velocity of liquid that flows out from the hole of a tank.
The cross-section of each hole is $0.01{\text{ }}{m^2}$ and the vertical distance between the holes is $1{\text{ }}m$. Let ${v_1}$ and ${v_2}$ be the velocities of efflux. Let the distance between the upper part of the tank and the $1$st hole be $h$. From the given figure we find out that,
${v_1} = \sqrt {2gh} - - - \left( 1 \right)$
As the distance between the $1$st hole and the $2$nd hole is $h$.
Then, ${v_2} = \sqrt {2g\left( {h + 1} \right)} - - - - \left( 2 \right)$
Let the rate of flow of liquid from the $1$st hole be ${Q_1}$ and the $2$nd hole is ${Q_2}$.
The formula for the rate of flow of liquid is,
$Q = Av = \dfrac{d}{{dt}}\left( V \right) - - - - - \left( 3 \right)$ where $Q =$ rate of flow of liquid, $A =$ area of cross-section and $v =$ velocity of efflux and $V =$ volume.
Force can be defined also as the time rate of change of momentum.
$F = \dfrac{d}{{dt}}\left( {mv} \right)$ where $F =$ force, $m = mass$ and $v =$velocity.
We know, $m = \rho \times V$ where $\rho =$ density.
So, we can now write,
$F = v \times \dfrac{d}{{dt}}\left( m \right)$
Changing the mass into the form of density and volume,
$F = v \times \rho \times \dfrac{d}{{dt}}\left( V \right)$
$\dfrac{d}{{dt}}\left( V \right) = Q =$ time rate of flow.
Let the force and mass of liquid flown at the $1$st hole be ${F_1}$ and ${m_1}$ and the $2$nd hole is ${F_2}$ and ${m_2}$.
Total force $F = {F_2} - {F_1}$
So, we get,
$F = {v_2} \times \dfrac{d}{{dt}}\left( {{m_2}} \right) - {v_1} \times \dfrac{d}{{dt}}\left( {{m_1}} \right)$
Converting the mass and simplifying the equation we get,
$F = \rho \left[ {{v_2} \times \dfrac{d}{{dt}}\left( {{V_2}} \right) - {v_1} \times \dfrac{d}{{dt}}\left( {{V_1}} \right)} \right] \\\ \Rightarrow F = \rho \times \left[ {{v_2}{Q_2} - {v_1}{Q_1}} \right] \\\$
Substituting the values we get,
$F = 1000 \times \left[ {{A_2}v_2^2 - {A_1}v_1^2} \right]$
${A_2} = {A_1} = 0.01$and thus, putting the value of ${v_1}$ and ${v_2}$we get,
$F = 1000 \times 0.01 \times \left[ {2g\left( {h + 1} \right) - 2gh} \right] \\\ \Rightarrow F = 10 \times 2 \times 10 = 200 \\\$
So, the total force is $200{\text{ }}N$.

Note: It must be noted that the vertical distance between two holes is $1{\text{ }}m$ which does not imply total height. We have to use the force’s equation in terms of momentum and not in terms of acceleration and mass in this particular problem. The efflux velocity is dependent only upon height as the acceleration gravity for hole remains the same often.