Question

There are two boxes I and II. Box I contains 3 red and 6 black balls. Box II contains 5 red and ‘n’ black balls. One of the boxes, box I and box II is selected at random and a ball is drawn at random. The ball drawn is found to be red. If the probability that this red ball comes out from box II is $\dfrac{3}{5}$, find the value of ‘n’.

Answer 1

Hint: We will use Bayes theorem to solve this question. The formula of Bayes theorem is given as, $P\left( \dfrac{A}{B} \right)=\dfrac{P\left( A\cap B \right)}{P\left( B \right)}=\dfrac{P\left( A \right).P\left( \dfrac{B}{A} \right)}{P\left( B \right)}$, where P (A) is the probability of occurring of event A, P (B) is the probability of occurring of event B, $P\left( \dfrac{A}{B} \right)$ is the probability of A given B and $P\left( A\cap B \right)$ is the probability of occurring of both A and B.

Complete step-by-step answer:
It is given in the question that there are two boxes I and II. Box I contains 3 red and 6 black balls. Box II contains 5 red and ‘n’ black balls. One of the boxes, box I and box II is selected at random and a ball is drawn at random. And the ball drawn is found to be red. If the probability that this red ball comes out from box II is $\dfrac{3}{5}$ then we have been asked to find the value of ‘n’.
We will use Bayes theorem to find the value of n. We know that Bayes theorem can be written as,
$P\left( \dfrac{A}{B} \right)=\dfrac{P\left( \dfrac{B}{A} \right)P\left( A \right)}{P\left( B \right)}$, where P (A) is the probability of occurring of event A, P (B) is the probability of occurring of event B, $P\left( \dfrac{A}{B} \right)$ is the probability of A given B.
Let us consider the conditions given in the question, it can be shown as follows.

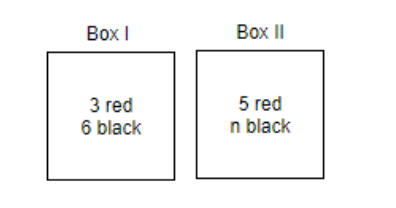
Let us assume $P\left( {{E}_{I}} \right)$ as the probability of selecting box I and $P\left( {{E}_{II}} \right)$ as the probability of selecting box II. We know that $P\left( {{E}_{I}} \right)=P\left( {{E}_{II}} \right)=\dfrac{1}{2}$ as we can select any one out of the two boxes at a time.
Let us consider P (A) to be the probability of choosing the red ball. And we know that the total number of balls present in box I is 3 + 6 = 9 balls. And the total number of balls present in box II is 5 + n balls.
So, we can write the probability of choosing the red ball from box II as follows.
$P\left( \dfrac{A}{{{E}_{I}}} \right)=\dfrac{\text{Number of red balls}}{\text{Total sample in boxI}}=\dfrac{3}{9}$
Now, we can write the probability of choosing red ball from box II that is,
$P\left( \dfrac{A}{{{E}_{II}}} \right)=\dfrac{\text{Number of red balls}}{\text{Total sample in boxI}}=\dfrac{3}{5+n}$
As all the red balls are given in box II, we can write, $P\left( \dfrac{{{E}_{II}}}{A} \right)=\dfrac{3}{5}$
Now, we know that Bayes theorem is, $P\left( \dfrac{A}{B} \right)=\dfrac{P\left( \dfrac{B}{A} \right)P\left( A \right)}{P\left( B \right)}$, on substituting the values in the formula, we get,

& P\left( \dfrac{{{E}_{II}}}{A} \right)=\dfrac{P\left( \dfrac{A}{{{E}_{II}}} \right)P\left( {{E}_{II}} \right)}{P\left( {{E}_{I}} \right).P\left( \dfrac{A}{{{E}_{I}}} \right)+P\left( {{E}_{II}} \right).P\left( \dfrac{A}{{{E}_{II}}} \right)} \\\ & \dfrac{3}{5}=\dfrac{\dfrac{5}{5+n}\times \dfrac{1}{2}}{\dfrac{1}{2}\times \dfrac{3}{9}+\dfrac{1}{2}\times \dfrac{5}{5+n}} \\\ & \dfrac{3}{5}=\dfrac{\dfrac{5}{10+2n}}{\dfrac{1}{6}+\dfrac{5}{10+2n}} \\\ & \dfrac{3}{5}=\dfrac{\dfrac{5}{10+2n}}{\dfrac{10+2n+30}{6\left( 10+2n \right)}} \\\ & \dfrac{3}{5}=\dfrac{5}{10+2n}\times \dfrac{6\left( 10+2n \right)}{40+2n} \\\ \end{aligned}$$ On cancelling the like terms, we get, $$\begin{aligned} & \dfrac{3}{5}=\dfrac{5\times 6}{40+2n} \\\ & \dfrac{1}{5}=\dfrac{5\times 2}{40+2n} \\\ \end{aligned}$$ On cross multiplying, we will get, $$\begin{aligned} & 40+2n=5\times 2\times 5 \\\ & 40+2n=50 \\\ \end{aligned}$$ On transferring the term containing n on side and all other terms on the other side, we get, 2n = 50 – 40 2n = 10 $n=\dfrac{10}{2}=5$ Therefore, we get the value of n as 5. Note: The possible mistakes that the students can make in this question is that some students may take the values of $P\left( \dfrac{A}{{{E}_{II}}} \right)=\dfrac{3}{5}$ and $P\left( {{E}_{II}} \right)=\dfrac{5}{3}$ which is wrong. As we had already calculated that $P\left( {{E}_{I}} \right)=P\left( {{E}_{II}} \right)=\dfrac{1}{2}$ and $P\left( \dfrac{A}{{{E}_{II}}} \right)=\dfrac{5}{5+n}$ where we had calculated n. So, it is recommended that the students do the calculations step by step and substitute the correct values.