Question

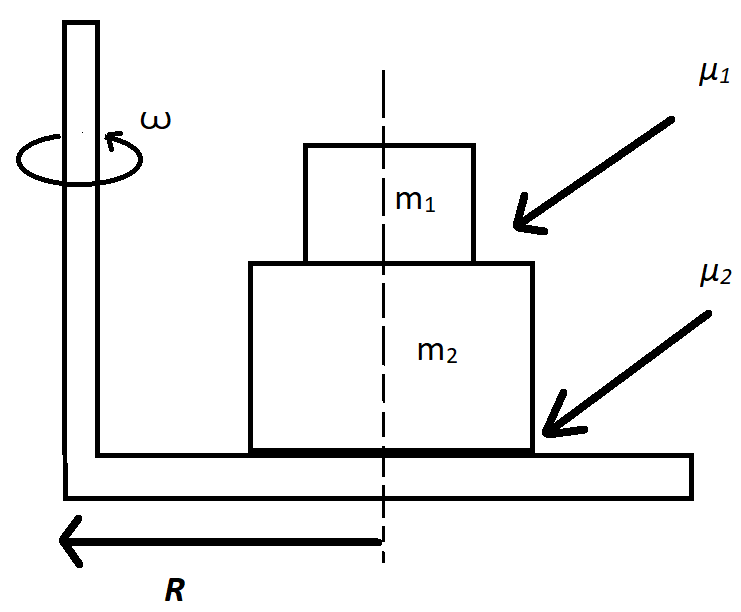
There are two blocks of masses ${m_1}$and ${m_2}$ is placed on ${m_2}$ on a table which is rotating with angular velocity $\omega$ about the vertical axis. The coefficients of friction between the block is ${\mu _1}$ and between ${m_2}$ and table is ${\mu _2}$ $\left( {{\mu _1} < {\mu _2}} \right)$. If the blocks are placed at distance R from the axis of rotation, for relative sliding between the surfaces in contact, find the:
a. Frictional force at the contacting surface
b. maximum angular speed $\omega$.

Answer 1

As we all know that from Newton’s third law of motion, if the first body applies a force on another body then another body also applies a reaction force on the first body and that reaction force is equal and opposite to the force applied.

Complete step by step answer:
We have to refer the below-given figure here,

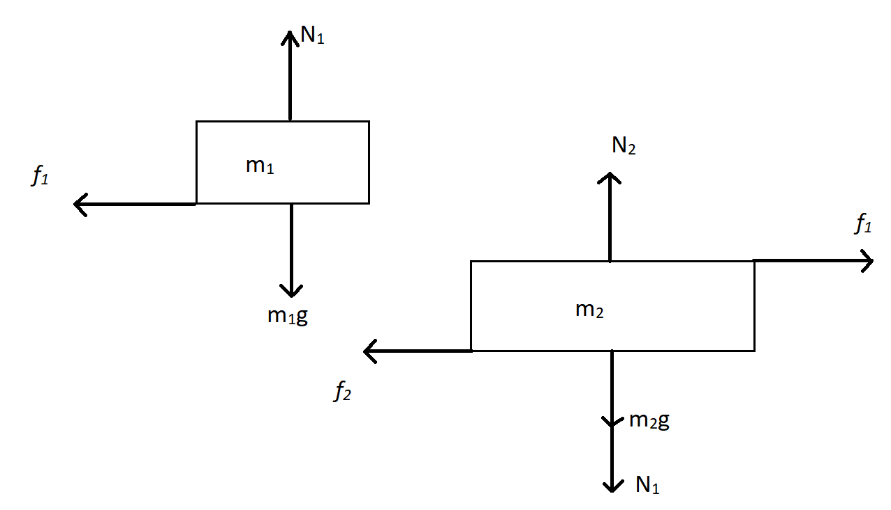
(a) Firstly we have to look at the body of mass ${m_1}$.
In this body ${f_1}$ is the frictional force acting between the two blocks and if the force of friction applied by mass ${m_2}$ on mass ${m_1}$ is ${f_1}$ then the same force of friction ${f_1}$ is applied by body ${m_1}$ on ${m_2}$. Therefore, the frictional force ${f_1}$ balances the centrifugal force ${m_1}\omega _1^2\,R$. So we can say that the equation becomes,
$\Rightarrow {f_1} = {m_1}\omega _{}^2\,R$…… (I)
Here, $\omega$ is the angular speed of rotation, and $R$ is the radius of rotation.
Therefore the frictional force at the contact surface is ${m_1}\omega _1^2\,R$.

(b) We can see that from the free body diagram of mass ${m_1}$, the normal reaction ${N_1}$ is balanced by the weight of the block. Therefore, it becomes,
${N_1} = {m_1}g$…… (II)
We also know that that,
${f_1} \leqslant \mu _1^{}{N_1}$…… (III)
Here ${\mu _1}{N_1}$ is the maximum limiting value of friction ${f_1}$. We can substitute ${N_1} = mg$ in equation (II) so it becomes,
${f_1} \leqslant {\mu _1}mg$…… (IV)
Now we can substitute ${f_1} = {m_1}\omega _{}^2\,R$ in equation (IV) and hence it becomes,
${m_1}\omega _{}^2\,R \leqslant {\mu _1}mg \\\ \Rightarrow \omega \leqslant \sqrt {\dfrac{{{\mu _1}g}}{R}} \\\$
So we can do it similarly for a block of mass ${m_2}$. For this block, the net frictional forces as shown in the free body diagram are balanced by the centrifugal force on this block.
${f_2} - {f_1} = {m_2}{\omega ^2}R$
$\Rightarrow {f_2} = {f_1} + {m_2}{\omega ^2}R$….. (V)
Here ${f_2}$ is the frictional force between ground and block of mass ${m_2}$. We can substitute ${f_1} = {m_1}\omega _{}^2\,R$ in equation in equation (V) to find the value of ${f_2}$.

$$\Rightarrow {f_2} = {m_1}{\omega ^2}R + {m_2}{\omega ^2}R \\\ \Rightarrow {f_2} = \left( {{m_1} + {m_2}} \right){\omega ^2}R \\\$$

We can also balance the vertical forces for a block of mass ${m_2}$.
$\Rightarrow {N_2} = {N_1} + {m_2}g$…… (VI)
Here, ${N_2}$ is the normal reaction for mass ${m_2}$.
We can substitute ${N_1} = {m_1}g$ in equation (VI) to find the value of ${N_2}$.
$\Rightarrow {N_2} = {m_1}g + {m_2}g \\\ \Rightarrow {N_2} = \left( {{m_1} + {m_2}} \right)g \\\$
We also know that that
${f_2} \leqslant \mu _2^{}{N_2}$…… (VII)
Here ${\mu _2}{N_2}$ is the maximum limiting value of friction ${f_2}$. We can substitute ${N_2} = \left( {{m_1} + {m_2}} \right)g$ in equation (VII) so it becomes,
${f_2} \leqslant \mu _2^{}\left( {{m_1} + {m_2}} \right)g$...... (VIII)
Now we can substitute ${f_2} = \left( {{m_1} + {m_2}} \right){\omega ^2}R$ in equation (VIII) to find the value of $\omega$.

$$\Rightarrow \left( {{m_1} + {m_2}} \right){\omega ^2}R \leqslant \mu _2^{}\left( {{m_1} + {m_2}} \right)g \\\ \Rightarrow {\omega ^2} \leqslant \dfrac{{\mu _2^{}g}}{R} \\\ \Rightarrow \omega \leqslant \sqrt {\dfrac{{\mu _2^{}g}}{R}} \\\$$

So we can see that as ${\mu _2} > {\mu _1}$ so we can say that $\omega = \sqrt {\dfrac{{\mu _2^{}g}}{R}}$.

**$\therefore$ The frictional force at the contact surface is ${m_1}\omega _1^2\,R$.
The maximum angular speed $\omega = \sqrt {\dfrac{{\mu _2^{}g}}{R}}$ **

Note:
Here in this question the case is given for relative sliding but if the question is given for no relative sliding then we can directly apply $\left( {{m_2} + {m_2}} \right){\omega ^2}R = {\mu _2}\left( {{m_1} + {m_2}} \right)g$. So from this relation we can find the angular velocity.