Question

There are three clubs $A,B,C$ in a town with $40,50,60$ members respectively. Ten people are members of all the three clubs. $70$ members belong to only one club. A member is randomly selected. Find the probability that he has membership of exactly two clubs.

Answer 1

We can solve this problem using set theory and probability. We can analyse the given data and express it using a venn diagram. Then we can solve for the favourable number. Using favourable number and total number we get the probability.

Formula used:
Probability of an event is obtained by dividing favourable number of outcomes by total number of outcomes.

Complete step-by-step answer:
Given $A,B,C$ clubs have members $40,50,60$ respectively.
Let it be $n(A),n(B),n(C)$.
$\Rightarrow n(A) = 40,n(B) = 50,n(C) = 60$
Also given ten people are members of all the three clubs.
$\Rightarrow n(A \cap B \cap C) = 10$
Also we have, $70$ members belong to only one club.
We can use a Venn diagram to express these data.

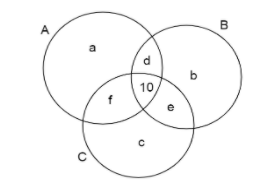
Here the three circles represent clubs $A,B,C$.
The small letters represent the number of members in each section.
Since we have $70$ members belong to only one club, we can write
$a + b + c = 70 - - - (i)$
Also we get from the diagram,
$\Rightarrow n(A) = a + d + f + 10,n(B) = b + d + e + 10,n(C) = c + e + f + 10$
Substituting we get,
$a + d + f + 10 = 40$
$b + d + e + 10 = 50$
$c + e + f + 10 = 60$
Simplifying we get,
$a + d + f = 30$
$b + d + e = 40$
$c + e + f = 50$
Adding these three equations we get,
$a + d + f + b + d + e + c + e + f = 30 + 40 + 50$
$\Rightarrow a + b + c + 2(d + e + f) = 120 - - - (ii)$
But from $(i)$ we have, $a + b + c = 70$
Substituting we get,
$\Rightarrow 70 + 2(d + e + f) = 120$
Subtracting $70$ from both sides we get,
$\Rightarrow 70 + 2(d + e + f) - 70 = 120 - 70$
$\Rightarrow 2(d + e + f) = 50$
Dividing both sides by $2$ we get,
$\Rightarrow \dfrac{2}{2}(d + e + f) = \dfrac{{50}}{2}$
Simplifying we get,
$\Rightarrow d + e + f = 25 - - - (iii)$
We can see from the diagram that this number represents the number of members exactly belong to two clubs,
So the favourable number here is $d + e + f = 25$
At the same time total number is represented by the sum $a + b + c + d + e + f + 10$
From $(i),(iii)$ we have, $a + b + c + d + e + f + 10 = 70 + 25 + 10 = 105$
$\Rightarrow {\text{Total number of persons = 105}}$
Now the probability is a favourable number divided by total number.
So we have $probability = \dfrac{{25}}{{105}}$
Cancelling $5$ from the numerator and denominator we get the required probability as $\dfrac{5}{{21}}$.
Therefore, the probability of members belong to exactly two clubs is $\dfrac{5}{{21}}$.

Note: Here it is important to interpret the given data. Using the diagram we could express the data and identify the required one. So we could easily calculate the probability.