Question

There are four lines in a plane no two of which are parallel. The maximum number of points in which they can intersect is:
A. 4
B. 5
C. 6
D. 7

Answer 1

First of all this is a very simple and a very easy problem. To solve this problem we have to know about the concept of permutations and combinations. But here a simple concept is used. Although this problem deals with combinations only. Here factorial of any number is the product of that number and all the numbers less than that number till 1.
$\Rightarrow n! = n(n - 1)(n - 2).......1$

Complete step-by-step solution:
Here given that there are four lines, which are not parallel.
Here also given that no two lines are parallel, which means there is not a single one in the four lines which is parallel to another line in the total of 4 lines.
So these four lines are not parallel to any of the lines, and also not parallel to any line among the four lines.
We have to find the maximum number of points where there is a scenario of their intersection.
So we are asked to find the maximum number of intersection points, when these four non-parallel lines intersect.
Here visualizing it, the four lines which are not parallel to any of the line, as given below:

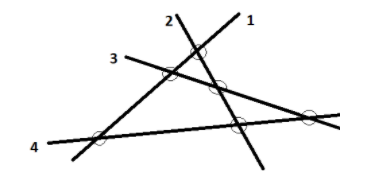
Here we can see that in the above figure, there are four lines which are not parallel to any of them. So here there are 6 points of intersection, as observed.
To find the maximum number of points of intersection can also be done by the combinations method.
Given four non-parallel lines, and no two lines are parallel to each other, hence the maximum no. of intersection points is given by:
$\Rightarrow {}^4{C_2} = \dfrac{{4!}}{{(4 - 2)!2!}}$
$\Rightarrow {}^4{C_2} = \dfrac{{4 \times 3}}{2}$
$\Rightarrow {}^4{C_2} = 6$
Hence the maximum no. of points of intersection are 6.

Option C is the correct answer.

Note: Please note that this problem can be done in either of the methods, either by finding the points of intersection by visual representation or by using the method of combinations. But mostly the preferred method is the method of combinations, as there may be human errors in the visual representation method. Here the combinations formula used is, given there are n lines and no r lines are not parallel, then the points of intersection is given by ${}^n{C_r} = \dfrac{{n!}}{{(n - r)!r!}}$