Question

There are four concentric shells A, B, C and D of radii $a$, $2a$, $3a$ and $4a$ respectively. Shell B and D are given charges $+ q$ and $- q$ respectively. Shell C is now earthed. The potential difference ${V_A} - {V_C}$ is $k = \dfrac{1}{{4\pi {\varepsilon _o}}}$:
(A) $\dfrac{{kq}}{{2a}}$
(B) $\dfrac{{kq}}{{3a}}$
(C) $\dfrac{{kq}}{{4a}}$
(D) $\dfrac{{kq}}{{6a}}$

Answer 1

Hint
We need to find the potential at shell C and then equate that value to zero. From there we can find the charge induced on C. Therefore, by calculating the value of the potential at the shells A and C and we can find the difference in their potential.

Formula Used: In this solution, we will be using the following formula
$V = \dfrac{{kq}}{d}$
where $V$ is the potential
$k = \dfrac{1}{{4\pi {\varepsilon _o}}}$ where ${\varepsilon _o}$ is the permittivity in free space, $q$ is the charge and $d$ is the distance.

Complete step by step answer
In this case there are 4 concentric shells A, B, C, and D of radius $a$, $2a$, $3a$ and $4a$. A charge $q$ is placed on shell B and $- q$ is placed on the shell D. So we can draw the figure as,

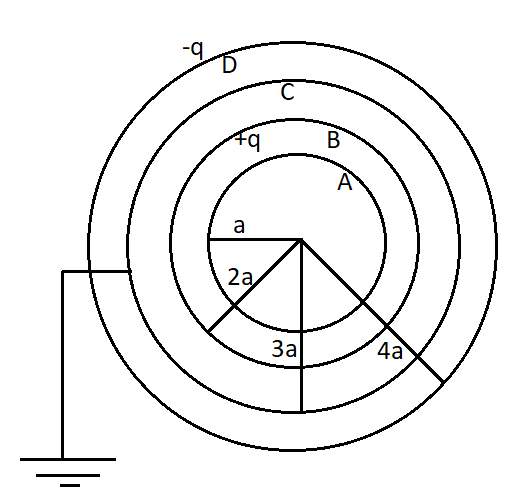
The electric potential due to a charge can be given by the formula,
$V = \dfrac{{kq}}{d}$
Now the potential on the shell C due to the charges placed on the shells D end B is,
${V_c} = \dfrac{{kq}}{{3a}} + \dfrac{{kq'}}{{3a}} - \dfrac{{kq}}{{4a}}$
where $q'$ is the charge induced on C.
And the potential on the surface of A is,
${V_A} = \dfrac{{kq}}{{2a}} + \dfrac{{kq'}}{{3a}} - \dfrac{{kq}}{{4a}}$
Now the shell C is grounded. So the potential on C will be 0. That is, ${V_c} = 0$.
So equating the equation we get,
$0 = \dfrac{{kq}}{{3a}} + \dfrac{{kq'}}{{3a}} - \dfrac{{kq}}{{4a}}$
We can cancel the $k$ and $a$ from the numerator and denominator of all the terms.
So we get,
$0 = \dfrac{q}{3} + \dfrac{{q'}}{3} - \dfrac{q}{4}$
Therefore taking the term containing $q'$ to one side,
$\dfrac{{q'}}{3} = \dfrac{q}{4} - \dfrac{q}{3}$
On the R.H.S taking LCM, we find $q'$ as,
$q' = \dfrac{{\left( {3 - 4} \right)}}{{12}}3q$
On doing the calculation we get
$\Rightarrow q' = - \dfrac{q}{4}$
Now putting this value of $q'$ in the equation for ${V_A}$ we get
${V_A} = \dfrac{{kq}}{{2a}} - \dfrac{{k\dfrac{q}{4}}}{{3a}} - \dfrac{{kq}}{{4a}}$
$\Rightarrow {V_A} = \dfrac{{kq}}{{2a}} - \dfrac{{kq}}{{12a}} - \dfrac{{kq}}{{4a}}$
On doing the LCM and calculating further we get3
${V_A} = \dfrac{{6kq - kq - 3kq}}{{12a}} = \dfrac{{2kq}}{{12a}}$
Hence we get the value of the potential at the surface of A as,
${V_A} = \dfrac{{kq}}{{6a}}$
Since ${V_C} = 0$
Therefore ${V_A} - {V_C} = \dfrac{{kq}}{{6a}}$
This is the difference in potential. So the correct option is D.

Note
The electric potential at a point in an electric field is the amount of work that is done in bringing a unit positive charge from infinity to that point. And when a body is charged it can attract and repulse an oppositely charged body. This shows the ability of a charged body to do work. This ability is called the potential of that body.